The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Vectors Vector Algebra Corollaries
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Corollaries

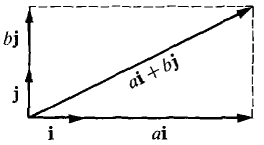
COROLLARY 1

The vector with components a and b is ai + bj

PROOF

ai is the vector from (0,0) to (a, 0), bj is the vector from (0,0) to (0, b). Therefore the sum ai + bj is the vector from (0,0) to (a, b) (Figure 10.1.17).

10_vectors-42.gif

Figure 10.1.17

Sums, differences, scalar multiples, and lengths of vectors can easily be computed using the basis vectors and components. The necessary formulas are given in the next corollary.

COROLLARY 2

Let A = a1i + a2j and B = b1i + b2j be vectors and let c be a scalar.

(i) A + B = (a1 + b1)i + (a2 + b2)j. (ii) A - B = (a1 - b1)i + (a2 - b2)j.

(iii) cA = (ca1)i + (ca2)j. (iv) 10_vectors-43.gif

For example,

(i) is shown by the computation

A + B = (a1i + a2j) + (b1i + b2j) = (a1i + b1i) + (a1j + b2j) = (a1 + b1)i + (a2 + b2)j.

It is illustrated in Figure 10.1.18.

10_vectors-44.gif

Figure 10.1.18

Example 4
Example 5

Home Vectors Vector Algebra Corollaries

Last Update: 2006-11-07