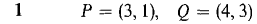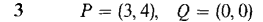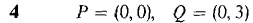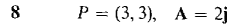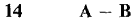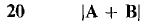Problems

In Problems 1-4 find the vector represented by the directed line segment

In Problems 5-8 find the point Q such that A is the vector from P to Q.

In Problems 9-32, find the given vector or scalar, where

A = i - 2j, B = -4i + 3j, C = 3i.

24            The vector D such that A + 2D = B.

25            The vector D such that 2A + 4D = C - 3B.

26            The unit vector and direction cosines of A.

27            The unit vector and direction cosines of B.

28            The unit vector and direction cosines of C.

29            The angle between A and B.

30            The angle between A and C.

31             The angle between B and C.

32            The angle between -B and C.

33            An object initially has position vector P = 3i + 5j and is displaced by the vector A = 4i - 2j. Find its new position vector.

34            An object is displaced first by the vector A = -i - 2j and then by the vector B = 4i - j. Find the total displacement vector.

35            Find the displacement vector necessary to change the position vector of an object from P = -3i + 6j to Q = 5i + 4j.

36            Three forces are acting on an object, with vectors

F = i + 3j, G = 2i, H = -2i - j. Find the total force on the object.

37            Three forces are acting on an object which is at rest. The first two forces arc

F₁ = -6i + 9j. F₂ = 10i - 3j. Find the third force F₃.

38            An object of mass 10 is being accelerated so that its acceleration vector is A = 5i - 6j. Find the total force acting on the object.

39            An object is displaced by the vector 3i - 4j. Find the distance it is moved.

40            An object has the velocity vector V = i - j. Find its speed.

41             A trader initially has the commodity vector A = 3i + j and buys the commodity vector B = i + 2j. Find his new total commodity vector.

42            Two traders initially have commodity vectors A₀ = 4i + j, B₀ = 3i + 6j. After trading with each other, trader A has the commodity vector A_l = 3i + 3j. Find the new commodity vector B₁ of trader B.

43            A trader initially has the commodity vector A = 15i + 12j and sells the commodity vector 5i + 10j. Find his new commodity vector.

44            A pair of commodities initially has the price vector P = 6i + 9j. Due to inflation all prices are increased by 10%. Find the new price vector.

45            Find the vector with length 4 and direction cosines (-√2/2. √2,2).

46             Find the vector with length 4 and direction cosines (-1, 0).

47             Find the vector with length 10 and direction cosines (3/5, 4/5).

In Problems 48-50 find the vectors counterclockwise around the perimeter of the polygon with the given vertices.

48            (0, 0), (1, 0), (0, 1).

49            (1, 1), (3, 0), (5, 2), (0, 4).

50            The regular hexagon inscribed in the unit circle x² + y² = 1 with the initial vertex (1, 0).

51             Use the Triangle Inequality to prove the following.

|A - B| ≤ |A| + |B|, |A| - |B| ≤ |A + B|,

|A + B + C| ≤ |A| + |B| + |C|.

52            Prove that for every nonzero vector A and positive scalar x. there are exactly two scalar multiples tA of length s.

53             Prove that two nonzero vectors A and B have the same direction cosines if and only if B = tA for some positive t.

54            Prove the Commutative Law for vector addition.

55             Prove the Distributive Laws for scalar multiples.

56             Prove the Triangle Inequality. Hint: Assume

and get a contradiction. This is done by squaring both sides, simplifying, and then squaring and simplifying again.