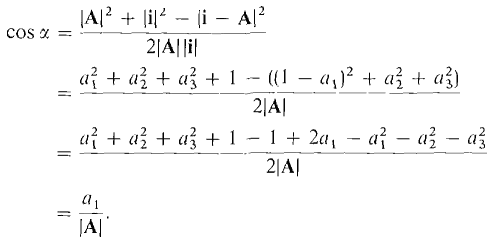Angle Between Two Vectors - Direction Cosines

The Law of Cosines gives us a formula for the angle between two vectors in space. In fact, we shall use the Law of Cosines to define the angle between two vectors.

One can prove from the Triangle Inequality that the above quantity is always between -1 and 1, and therefore is the cosine of some angle θ (Problem 42 at the end of this section).

Example 2: Finding an Angle between Two Vectors

The direction angles of a nonzero vector A in space are the three angles α, β, γ between A and i, j, k respectively. The cosines of the direction angles are called the direction cosines of A. Let us compute the direction cosines in terms of the components of A.

The computations for β and γ are similar. Thus