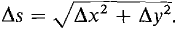The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Partial Differentiation Contionuous Functions of Two or More Variables Contionuous Functions of Two or More Variables
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Contionuous Functions of Two or More Variables

11.2 CONTINUOUS FUNCTIONS OF TWO OR MORE VARIABLES

Two points (xx, yt) and (x2,y2) in the hyperreal plane are said to be infinitely close,

(x1, y1) ≈ (x2, y2),

if both x1 ≈ x2 and y1 ≈ y2.

If

Δx = x2 - x1, Δy = y2 - y1,

then the distance between (x1, y1 and (x2, y2) is

11_partial_differentiation-101.gif

LEMMA 1

Two points are infinitely close to each other if and only if the distance between them is infinitesimal.

This lemma can be seen from Figure 11.2.1. (An easy proof of the lemma in terms of vectors was given in Section 10.8.)

11_partial_differentiation-102.gif

Figure 11.2.1
Home Partial Differentiation Contionuous Functions of Two or More Variables Contionuous Functions of Two or More Variables

Last Update: 2010-11-25