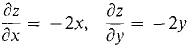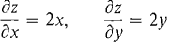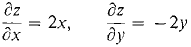The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Partial Differentiation Maxima and Minima Critical Point Theorem
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Critical Point Theorem

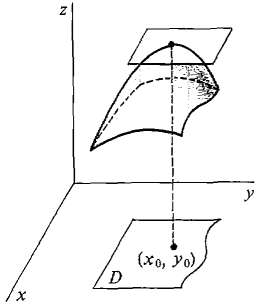
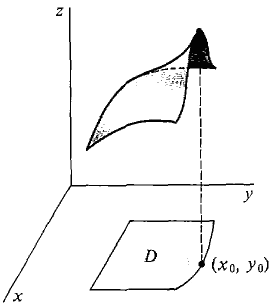
CRITICAL POINT THEOREM

Suppose the domain of z = f(x, y) is a closed region D and f is smooth at every interior point of D. If f has a maximum or minimum at i(x0,y0), then either

(i) fx(x0, y0) = 0 and fy (x0,y0) = 0, or

(ii) (x0, y0) is a boundary point of D.

11_partial_differentiation-455.gif 11_partial_differentiation-456.gif

Case (i) Interior Maximum

Case (ii) Boundary Maximum
Figure 11.7.2 Critical Point Theorem

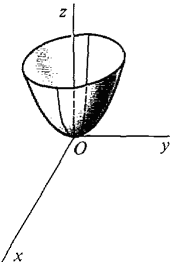
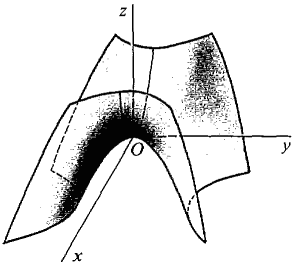
Figure 11.7.2 illustrates the two cases when f has a maximum at (x0, y0). An interior point where both partial derivatives are zero is called a critical point. Thus a critical point is a point where the tangent plane is horizontal. On the graph of a surface, an interior point looks like a mountain summit if it is a maximum and a valley bottom if it is a minimum. The theorem states that every interior maximum or minimum is a critical point. An interesting kind of critical point which is neither a maximum nor a minimum is a saddle point, which looks like the summit of a pass between two mountains.

Function

Partials

Critical Point

Type

z = -(x2 + y2)

11_partial_differentiation-452.gif

(0,0)

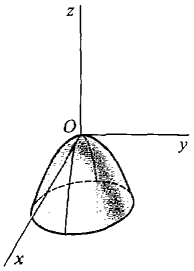
11_partial_differentiation-449.gif
Maximum

z = x2 + y2

11_partial_differentiation-453.gif

(0,0)

11_partial_differentiation-450.gif
Minimum

z = x2 - y2

11_partial_differentiation-454.gif

(0,0)

11_partial_differentiation-451.gif
Saddle Point
Table 11.7.1. Figure 11.7.3

Table 11.7.1 gives three simple examples of critical points, one maximum, one minimum, and one saddle point. They are illustrated in Figure 11.7.3.

PROOF OF THE CRITICAL POINT THEOREM

Suppose f has a maximum at an interior point (x0, y0) of D. (x0, y0) is not a boundary point so we must prove

(i). The function

g(x) = f(x, y0)

is differentiable and has a maximum at x0.

By the Critical Point Theorem for one variable,

g'(x0) = fx(x0, y0) = 0.

Similarly

fy(x0, y0) = 0.
Home Partial Differentiation Maxima and Minima Critical Point Theorem

Last Update: 2006-11-05