| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Maxima and Minima Maxima and Minima  Examples Examples  Example 7 Example 7 |
||||||||||||||||||||||||






|
||||||||||||||||||||||||
Example 7
Find the dimensions of the box of volume one without a top which has the smallest area (if there is one). The box is sketched in Figure 11.7.13.
Figure 11.7.13
Figure 11.7.15 CONCLUSION A is infinite and hence greater than 22/3 + 25/3 on the boundary of E. Therefore A has a minimum at the critical point
The box has dimensions
|
||||||||||||||||||||||||
Home  Partial Differentiation Partial Differentiation  Maxima and Minima Maxima and Minima  Examples Examples  Example 7 Example 7 |
||||||||||||||||||||||||
Last Update: 2006-11-15


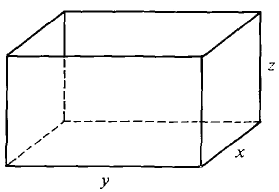
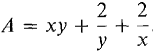


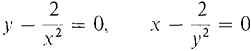
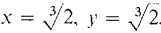 where A = 22/3 + 2·2-1/3 + 2·2-1/3 = 22/3 + 25/3.
where A = 22/3 + 2·2-1/3 + 2·2-1/3 = 22/3 + 25/3.