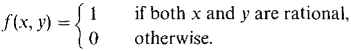| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Extra Problems for Chapter 11 Extra Problems for Chapter 11 |
|






|
|
Extra Problems for Chapter 11
In Problems 1-4, make a contour map and sketch the surface.
5 Find the largest set you can on which f(x, y) = y + 1/x2 is continuous. 6 Find the largest set you can on which f(x, y) = 7 Find the largest set you can on which f(x, y) = ln (1/x + 1/y) is continuous. 8 Find the largest set you can on which f(x, y, z) = (ln (x + y))/z is continuous. 9 Find the partial derivatives of f(x, y) = ax - by. 10 Find the partial derivatives of f(x, y) = a1 sin (b1x) + a2 cos (b2 y). 11 Find the partial derivatives of z = ln x/ln y. 12 Find the partial derivatives of w = (x - y)ez. 13 Find the increment and total differential of z = l/x + 2/y. 14 Find the increment and total differential of z = 15 Find the tangent plane of z = x3y + 4 at (2,0). 16 Find the tangent plane of z = arcsin (xy) at (3, ¼). 17 Find dz/dt by the Chain Rule where z = log(2r+1) (3t + 2). 18 Find ∂z/∂s and ∂z/∂t where z = x/y, x = ex+1, y = as + bt. 19 A particle moves in space so that dx/dt = z cos x, dy/dt = z sin y, dz/dt = 1. Find the rate of change of the distance from the origin when x = 0, y = 0, z = 1. 20 A company finds that it can produce x units of item 1 at a total cost of x + 100√x dollars, and y units of item 2 at a total cost of 20y - √y dollars. Moreover, x units of item 1 and y units of item 2 can be sold for a total revenue of 10x + 30y - xy/100 dollars. If z is the total profit (revenue minus cost), find ∂z/∂x and ∂z/∂y, the partial marginal profit with respect to items 1 and 2. 21 Find the tangent line and slope of x4 + y4 = 17 at (2,1). 22 Find the tangent plane to the surface x4 + y4 + z2 = 18 at (1, 2, 1). 23 Find the maxima and minima of z = x2 + y2 - 2x - 4y + 4, 0 ≤ x ≤ 3, x ≤ y ≤ 3. 24 Find the maxima and minima of
25 Determine whether the surface z = logx y, x > 1, y > 0 has any maxima or minima. 26 Find the dimensions of the rectangular box of maximum volume such that the sum of the areas of the bottom and sides is one. 27 Find all second partial derivatives of z = arctan (xy). 28 Find all second partial derivatives of w = (x2 - y2)z. 29 Find ∂2z/∂r2 if z = f(x, y), x = r cosh θ, y = r sinh θ. 30 Let f(x) be continuous for a < x < b. Prove that the function F(u, v) = 31 Prove that f(x, y) is continuous at (a, b) if and only if the following ε, δ condition holds. For every real ε > 0 there is a real δ > 0 such that whenever (x, y) is within δ of (a, b), f(x, y) is within ε of f(a, b). 32 Let Prove that f is discontinuous at every point. 33 Prove that lim(x,y)→(a,b) f(x, y) = L if and only if for every real ε > 0 there is a real δ > 0 such that whenever (x, y) is different from but within δ of (a, b), f(x, y) is within ε of L. (See Problems for Section 11.2.) 34 Prove that the following are equivalent.
35 Prove that the following are equivalent.
36 A function z = f(x, y) is said to be differentiable at (x, y) if it satisfies the conclusion of the Increment Theorem. That is, whenever Δx and Δy are infinitesimal, Δz = dz + ε1 Δx + ε2 Δy for some infinitesimals ε1 and ε2 which depend on Δx and Δy. Prove the Chain Rule
assuming only that the functions z = f(x, y), x = g(r), and y = h(t) are differentiable. 37 Prove that the function f(x, y) = |xy| is differentiable but not smooth at (0, 0). 38 A smooth function z = f(x, y) is said to be homogeneous of degree n if (1) f(fx, fy) = f' f(x,y) for all x, y, and t. Prove that if z = f(x, y) is homogeneous of degree n then
Hint: Differentiate Equation 1 with respect to t and set t = 1. 39 Suppose f(x, y) has continuous second partial derivatives and that ∂2f/∂x ∂y is identically zero (i.e., zero at every point (x, y)). Prove that f(x, y) = g(x) + h(y) for some functions g and h. 40 Find all functions f(x, y) all of whose second partial derivatives are identically zero.
|
|
Home  Partial Differentiation Partial Differentiation  Extra Problems for Chapter 11 Extra Problems for Chapter 11 |
|
Last Update: 2010-11-25


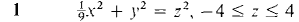
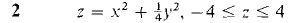


 is continuous.
is continuous.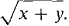
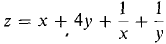

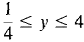
 is continuous whenever u and v are in (a, b).
is continuous whenever u and v are in (a, b).