Double Riemann Sum - Rectangular Region

We now define the double Riemann sum and use it to give a precise definition of the double integral. We first consider the case where D is a rectangle

a₁ ≤ x ≤ a₂- b₁ ≤ y ≤ b₂,

shown in Figure 12.1.5.

Figure 12.1.5

Let Δx and Δy be positive real numbers. We partition the interval [a₁,a₂] into subintervals of length Δx and [b₁, b₂] into subintervals of length Δy The partition points are

x₀ = a₁, x₁ = a₁ + Δx, x₂ = a₁+ 2 Δx,..., x_n = a₁ + n Δx,

y₀ = b₁, y₁ = b₁ + Δy, y₂ = b₁+ 2 Δy,..., y_p = b₁ + p Δy

where

x_n, < a₂ ≤ x_n, + Δx,

y_p < b₂ ≤ y_p + Δy.

If Δx and Δy do not evenly divide a₂ - a₁ and b₂ - b₁,there will be little pieces left over at the end. We have partitioned the rectangle D into Δx by Δy sub-rectangles with partition points

(x_k , y_l), 0 ≤ k ≤ n, 0 ≤ l ≤ p,

as in Figure 12.1.6.

Figure 12.1.6

The Double Riemann Sum for a rectangle D is the sum

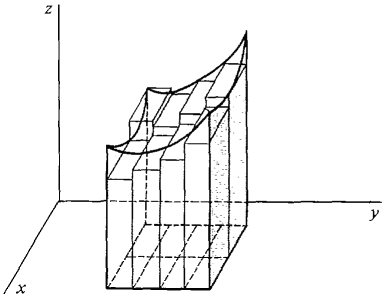
This is the sum of the volume of the rectangular solids with base Δx Δy and height

f(x_k,y_l).

As we can see from Figure 12.1.7,

approximates the volume of the solid over D between z = 0 and z = f(x, y).

Figure 12.1.7 Double Riemann Sum