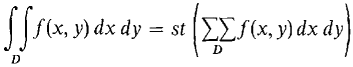Infinite Double Riemann Sum

Given the function f(x, y) and the region D, the double Riemann sum

is a real function of Δx and Δy. When we replace Δx and Δy by positive infinitesimals dx and dy (Figure 12.1.12), we obtain (by the Function Axiom) the infinite double Riemann sum

Figure 12.1.12: Infinite Double Riemann Sum

The infinite double Riemann sum is in general a hyperreal number. Intuitively, it is equal to the sum of the volumes of infinitely many rectangular solids of infinitesimal base dx dy and height f(x_K,y_L). The double integral is defined as the standard part of the infinite double Riemann sum. The following lemma, based on our Permanent Assumption for Chapter 12, shows that this sum has a standard part.

We omit the proof, which is similar to the proof that single Riemann sums are finite. We are now ready to define the double integral.

Here is a list of properties of the double integral. Each property is analogous to a property of the single integral given in Chapter Four and has a similar proof.

INDEPENDENCE OF dx AND dy

ADDITION PROPERTY

CYLINDER PROPERTY