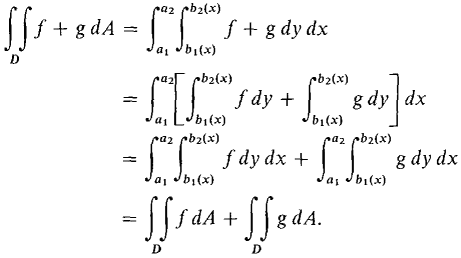| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Multiple Integrals Iterated Integrals Constant, Sum, and Inequality Rules |
|
 Search the VIAS Library | Index
|
  |
Constant, Sum, and Inequality Rules
The Constant, Sum, and Inequality Rules for double integrals follow easily from the corresponding rules for single integrals, using the Iterated Integral Theorem. Constant Rule
Sum Rule
Inequality Rule If f(x, y) ≤ g(x, y) for all (x, y) in D,
PROOF As an illustration we prove the Sum Rule.
The Iterated Integral Theorem gives another proof that the area of D is equal to the double integral of 1 over D. By definition of area between two curves,
Using iterated integrals,
|
|
| Home Multiple Integrals Iterated Integrals Constant, Sum, and Inequality Rules |
|
Last Update: 2006-11-05