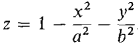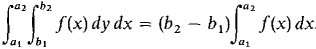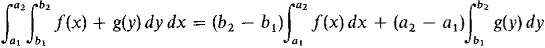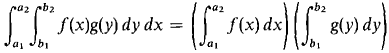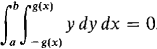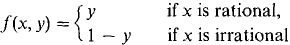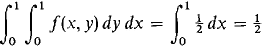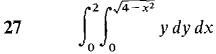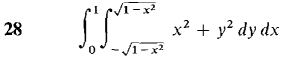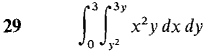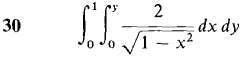| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Iterated Integrals Iterated Integrals  Problems Problems |
|






|
|
Problems
In Problems 1-16, evaluate the double integrals (compare these with the problems from Section 12.1).
In Problems 17-24, evaluate the iterated integral. Then check your answer, by evaluating in the other order.
In Problems 25-30 evaluate the iterated integral.
In Problems 31-38, find inequalities which describe the given region D, and write down an iterated integral equal to ∫∫D f(x, y) dA. 31 The triangle with vertices (0, 0), (5, 0), (0, 5). 32 The triangle with vertices (1, - 2), (1, 4), (5, 0). 33 The circle of radius 2 with center at the origin. 34 The bottom half of the circle of radius 1 with center at (2, 3). 35 The region bounded by the parabola y = 4 - x2 and the line y = 3x. 36 The region above the parabola y = x2 and inside the circle x2 + y2 = 1. 37 The region bounded by the curves x = ½ and x = 1/(1 + y2). 38 The region bounded by the curves x = 12 + y2 and x = y4. 39 Find the volume of the solid over the region x2 + y2 ≤ 1 and between the surfaces z = 0, z = x2. 40 Find the volume of the solid over the region D:1 ≤ x ≤2,x ≤ y ≤ x2 and between the surfaces z = 0, z = y/x. 41 Find the volume of the solid between the surfaces z = 0, z = 2 + 3x - y, over the region 0 ≤ x ≤ 2, 0≤y≤x 42 Find the volume of the solid between the surfaces z = 0, z = 43 Find the volume of the solid bounded by the plane z = 0 and the paraboloid
44 Find the volume of the solid bounded by the three coordinate planes and the plane ax + by + cz = 1, where a, b, and c are positive. 45 Show that
46 Show that
47 Show that
48 Show that
49 Let
Show that:
|
|
Home  Multiple Integrals Multiple Integrals  Iterated Integrals Iterated Integrals  Problems Problems |
|
Last Update: 2006-11-25


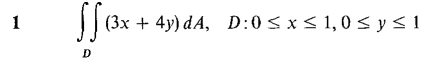
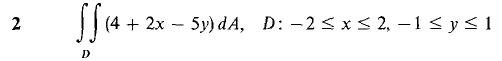
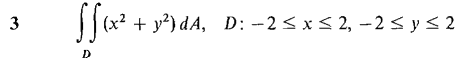
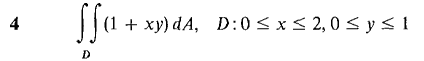
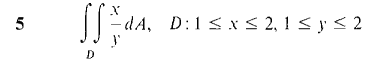
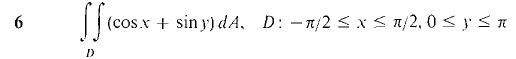
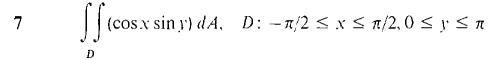
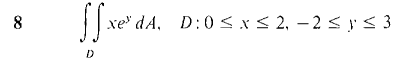
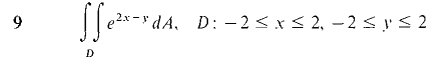
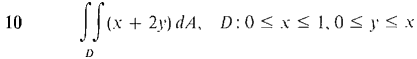
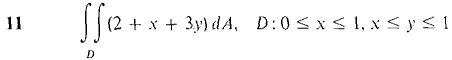
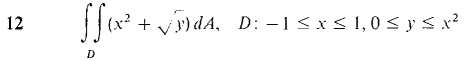
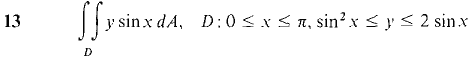
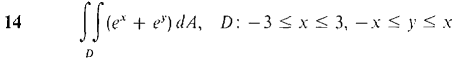
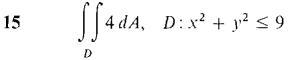
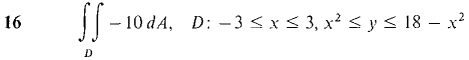
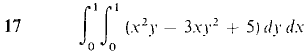
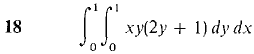
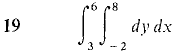
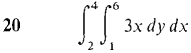
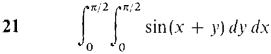
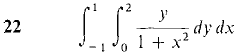
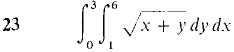
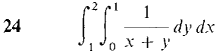
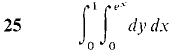
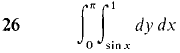
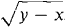 , over the region 0≤x≤l,x≤y≤l.
, over the region 0≤x≤l,x≤y≤l.