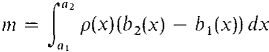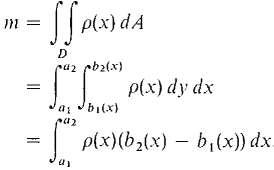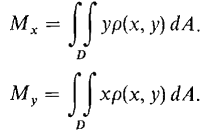| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Multiple Integrals Application to Physics Mass and Density |
|||
 Search the VIAS Library | Index
|
  |
||
Mass and Density
In this section we obtain double integrals for mass, center of mass, and moment of inertia. DEFINITION If a plane object fills a region D and has continuous density ρ(x, y), its mass is
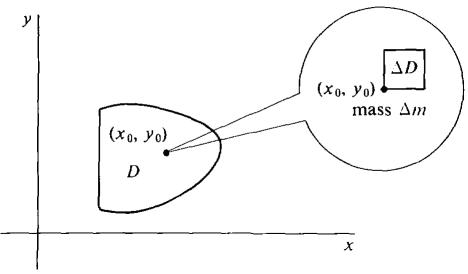
On an element of area ΔD, the density is infinitely close to ρ(x, y) (Figure 12.4.1). Therefore the mass is Δm ≈ ρ(x, y) ΔA (compared to ΔA). By the Infinite Sum Theorem m = ∫∫D p(x, y) dx dy.
Figure 12.4.1 In Chapter 6 we were able to find the mass of a plane object whose density ρ(x) depends only on x by a single integral,
Our new formula for mass reduces to the old formula in this case, for by the Iterated Integral Theorem,
Now we can find the mass of a plane object whose density ρ(x, y) depends on both x and y instead of on x alone.
DEFINITION A plane object which fills a region D and has continuous density ρ(x, y) has moments about the x and y axes given by
Mx and My are sometimes called first moments to distinguish them from moments of inertia (which are called second moments).
|
|||
| Home Multiple Integrals Application to Physics Mass and Density |
|
||
Last Update: 2010-11-25