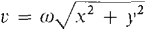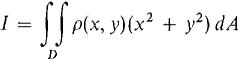Moment of Inertia

The second moment, or moment of inertia, of a point mass m about the origin is the mass times the square of the distance to the origin,

I = m(x² + y²).

The moment of inertia is related to the kinetic energy of rotation. A mass m moving at speed v has kinetic energy

KE = ½ mv².

Hence if m is rotating about the origin with angular velocity ω radians per second, its speed is

and

Thus moment of inertia is the rotational analogue of mass.

JUSTIFICATION

On an element of volume ΔD, the moment of inertia is

ΔI ≈ (x² + y²) Δm ≈ ρ(x, y)(x² + y²) ΔA (compared to ΔA).

The integral for I follows by the Infinite Sum Theorem.

Example 4: Moment of Inertia