| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Double Integrals in Polar Coordinates Double Integrals in Polar Coordinates  Examples Examples  Example 2 Example 2 |
|||||||






|
|||||||
Example 2
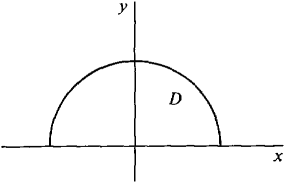
Find the mass and center of mass of a flat plate in the shape of a semicircle of radius one whose density is equal to the distance from the center of the circle.
Answer The point (x,y) is shown in Figure 12.5.10. Figure 12.5.10
|
|||||||
Home  Multiple Integrals Multiple Integrals  Double Integrals in Polar Coordinates Double Integrals in Polar Coordinates  Examples Examples  Example 2 Example 2 |
|||||||
Last Update: 2006-11-15



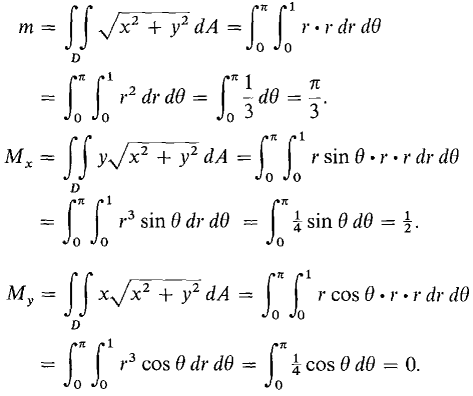
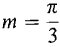 ,
,  ,
, 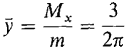 ~ 0.477.
~ 0.477.