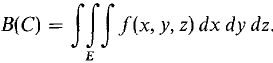Cylindrical Coordinates

In evaluating triple integrals it is sometimes easier to use cylindrical or spherical coordinates instead of rectangular coordinates.

A point (x, y, z) has cylindrical coordinates (θ, r, z) if

x = r cos θ, y = r sin θ, z = z.

That is, as we see in Figure 12.7.1, (θ, r) is a polar coordinate representation of (x, y), and z is the height above the (x, y) plane.

Figure 12.7.1 Cylindrical coordinates

The name cylindrical coordinates is used because the graph of the cylindrical coordinate equation r = constant is a circular cylinder as shown in Figure 12.7.2.

Figure 12.7.2

A cylindrical region is shown in Figure 12.7.3.

Figure 12.7.3 A cylindrical region  

The simplest kind of cylindrical region is the cylindrical box

α ≤ θ ≤ β, a ≤ r ≤ b, c₁ ≤ z ≤ c₂.

This is a cylinder whose base is a polar rectangle and whose upper and lower faces are horizontal, as in Figure 12.7.4.

Figure 12.7.4 A cylindrical box

The cylinder box

0 ≤ θ ≤ 2π, 0 ≤ r ≤ b, c₁ ≤ z ≤ c₂

is a cylinder whose base is a circle of radius b and whose top and bottom faces are horizontal (Figure 12.7.5).

Figure 12.7.5

The cylindrical box

0 ≤ θ ≤ 2π, a ≤ r ≤ b, c₁ ≤ z ≤ c₂

is a circular pipe with inner radius a and outer radius b (Figure 12.7.6).

Figure 12.7.6

To get a formula for the triple integral over a cylindrical region E, we use the Infinite Sum Theorem but take for ΔE an infinitely small cylindrical box instead of rectangular box.

CYLINDRICAL INTEGRATION FORMULA

Let E be the cylindrical region

α ≤ θ ≤ β, a(θ) ≤ r ≤ b(θ), c₁(θ, r) ≤ z ≤ c₂(θ, r).

The triple integral of f(x, y, z) over E is

To evaluate the triple integral we substitute

f(x, y, z) = f(r cos θ, r sin θ, z).

This is like the Polar Integration Formula but has an extra variable z. In the iterated integral we do not integrate f(x, y, z) but the product of f(x, y, z) and r.

The region C is shown in Figure 12.7.7.

Figure 12.7.7

We must prove that

Assume first that f(x, y, z) > 0 on E. For any (θ, r, z) region C₁ corresponding to a cylindrical region E₁, define

B has the Addition Property and is ≥ 0. An element of volume ΔC in the (θ, r, z) space has volume Δθ Δr Δz. As we can see from Figure 12.7.8, ΔC corresponds to a cylindrical box ΔE. ΔE is almost a rectangular box with sides r Δθ, Δr, and Δz, and volume r Δθ Δr Δz.

At any point of ΔE, f has value infinitely close to

f(x, r, z) = f(r cos θ, r sin θ, z).

Therefore

B(ΔC) ≈ f(x, y, z)r Δθ Δr Δz (compared to Δθ Δr Δz).

Figure 12.7.8

By the Infinite Sum Theorem

and by definition

The general case where f(x, y, z) is not always positive is dealt with as in the Polar Integration Formula proof.

When integrating over a solid region E whose base is a circle or polar rectangle, it is often easier to use cylindrical instead of rectangular coordinates.