| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Vector Calculus Directional Derivatives and Gradients Examples Example 5 |
|
 Search the VIAS Library | Index
|
  |
Example 5
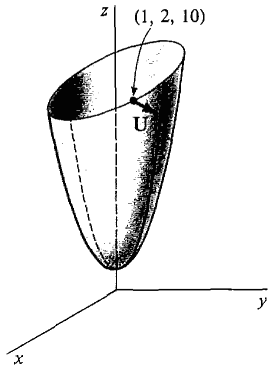
Find a unit vector normal to the surface z = x2 + 2y2 + 1 at (1,2,10) shown in Figure 13.1.8.
Figure 13.1.8 Let f(x, y, z) = -z + x2 + 2y2 + 1. By Corollary 2, grad f is normal to the given surface -z + x2 + 2y2 + 1 = 0. We compute grad f = 2xi + 4yj - k.
At (1,2,10), grad f = 2i + 8j - k. The required unit vector is found by dividing grad f by its length,
|
|
| Home Vector Calculus Directional Derivatives and Gradients Examples Example 5 |
|
Last Update: 2006-11-15