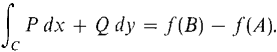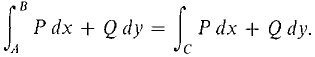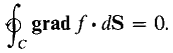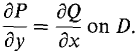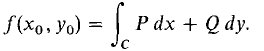The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Vector Calculus Independence of Path Theorem 2 (Path Independence Theorem)
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 2 (Path Independence Theorem)

THEOREM 2 (Path Independence Theorem)

Let Pi + Qj be a vector field such that ∂P/∂y = ∂Q/∂x and let A and B be two points of D.

(i) Let f be a potential function for Pi + Qj. For any piecewise smooth curve C from A to B,

13_vector_calculus-124.gif

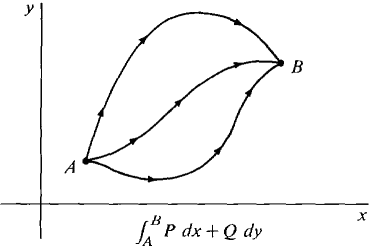
Since the line integral in this case depends only on the points A and B and not on the curve C (Figure 13.3.1), we write

13_vector_calculus-125.gif

(ii) g is a potential function for Pi + Qj if and only if g has the form

13_vector_calculus-126.gif

for some constant K.

13_vector_calculus-127.gif

Figure 13.3.1: Independence of path

Theorem 2 is important in physics. A vector field of forces which has a potential function is called a conservative force field. The negative of a potential function for a conservative force field is called a potential energy function. Gravity, static electricity, and magnetism are conservative force fields. Part (i) of the theorem shows that the work done by a conservative force field along a curve depends only on the initial and terminal points of the curve and is equal to the decrease in potential energy.

Mathematically, Theorem 2 is like the Fundamental Theorem of Calculus. It shows that the line integral of grad f along any curve from A to B is equal to the change in the value of f from A to B. When A = B, we have an interesting consequence :

If f(x, y) has continuous second partials then the line integral of the gradient of f around a simple closed curve is zero,

13_vector_calculus-128.gif

Using part (ii), we can find a potential function f(x, y) for a vector field Pi + Qj in three steps.

When to Use

13_vector_calculus-129.gif

Step 1

Choose an initial point A(a, b) in D.

Step 2

Choose and sketch a piecewise smooth curve C from A to an arbitrary point X(x0,y0).

Step 3

Compute f(x0, y0) by evaluating the line integral

13_vector_calculus-130.gif

We postpone the proof of Theorem 2 to the end of this section.
Home Vector Calculus Independence of Path Theorem 2 (Path Independence Theorem)

Last Update: 2006-11-22