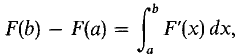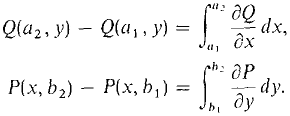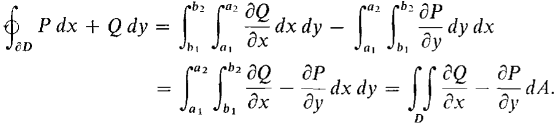Green's Theorem

Green's Theorem gives a relationship between double integrals and line integrals. It is a two-dimensional analogue of the Fundamental Theorem of Calculus,

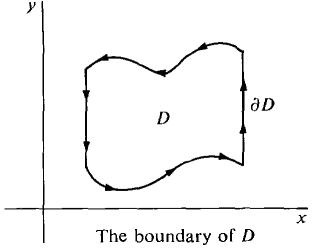
and shows that the line integral of F(x, y) around the boundary of a plane region D is equal to a certain double integral over D. Let D be a plane region

a₁ ≤ x ≤ a₂, b₁(x) ≤ y ≤ b₂(x).

The directed curve which goes around the boundary of D in the counterclockwise direction is denoted by ∂D and is called the boundary of D (Figure 13.4.1).

Figure 13.4.1

If b₁(x) and b₂(x) have continuous derivatives, ∂D will be a piecewise smooth curve and thus a simple closed curve (see Section 13.1).

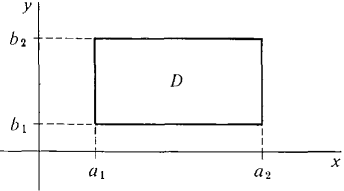
Figure 13.4.2

The second formula follows at once from the first formula by replacing P by -Q and Q by P. We shall prove the theorem only in the simplest case, where D is a rectangle.

The line integral around 3D is a sum of four partial integrals,

By the Fundamental Theorem of Calculus,

Therefore

We may apply Green's theorem to evaluate a line integral by double integration, or to evaluate a double integral by line integration.