| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Green's Theorem Green's Theorem  Curl and Divergence Curl and Divergence |
|






|
|
Curl and Divergence
Green's theorem has a vector form which is convenient for physical applications. We define two new functions obtained from a vector field, the curl and the divergence. DEFINITION Given a vector field F(x, y) = P(x, y)i + Q(x, y)j in the plane.
On the boundary 3D, the differential forms P dx + Q dy and -Q dx + P dy may be written in the vector form P dx + Q dy = F · T ds, -Q dx + P dy = F · N ds, where T = unit tangent vector to 3D, T ds = dxi + dyj, and N = unit outward normal vector to 3D, N ds = dyi - dxj T and N are shown in Figure 13.4.7.
Figure 13.4.7 Substituting the vector notation into the original form of Green's Theorem, we get the following. GREEN'S THEOREM (Vector Form) Given a vector field F(x, y) = Pi + Qj on a region D with a piecewise smooth boundary,
The physical meaning of Green's theorem can be explained in terms of the flow of a fluid (a liquid or gas). Let the vector field F(x, y) represent the rate and direction of fluid flow at a point (x, y) in the plane. Consider a plane region D and element of area ΔD containing (x, y) (Figure 13.4.8).
Figure 13.4.8 We first explain the formula
The line integral
Figure 13.4.9 When we apply Green's theorem to an element of area ΔD we get
Thus the curl of F at (x, y) is equal to the circulation per unit area at (x, y). If curl F is identically zero, the fluid flow F is called irrotational. By the Exactness Criterion, F is irrotational if and only if P dx + Q dy is an exact differential. The circulation of an irrotational field around any 3D is zero. Next we explain the formula
The line integral
Figure 13.4.10 When we apply this to ΔD we get
Therefore the divergence of F at (x, y) is the net rate of flow of fluid away from (x, y), and is equal to the rate of decrease in density at (x, y). Positive divergence means that the density is decreasing, and negative divergence means that the density is increasing. If div F is identically zero, the fluid flow is called solenoidal, or incompressible. By the Exactness Criterion, F is incompressible if and only if -Q dx + P dy is an exact differential. The flux of an incompressible field across any 3D is zero.
|
|
Home  Vector Calculus Vector Calculus  Green's Theorem Green's Theorem  Curl and Divergence Curl and Divergence |
|
Last Update: 2010-11-25








 of the flow component in the direction tangent to the boundary is called the circulation of
of the flow component in the direction tangent to the boundary is called the circulation of 
 (compared to ΔA).
(compared to ΔA).
 of the flow component in the direction of the outward normal vector is called the flux across 3D. The flux is the net rate at which fluid is flowing from inside D across the boundary and is therefore equal to the rate of decrease of the mass inside D. Green's Theorem states that the flux of F across the boundary of D equals the integral of the divergence of F over D (Figure 13.4.10).
of the flow component in the direction of the outward normal vector is called the flux across 3D. The flux is the net rate at which fluid is flowing from inside D across the boundary and is therefore equal to the rate of decrease of the mass inside D. Green's Theorem states that the flux of F across the boundary of D equals the integral of the divergence of F over D (Figure 13.4.10).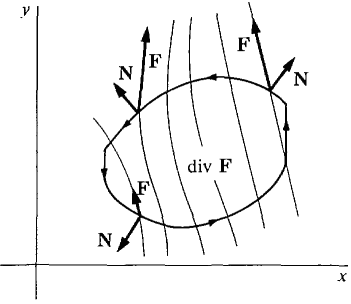
 (compared to ΔA).
(compared to ΔA).