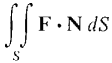| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Vector Calculus Surface Area and Surface Integrals Oriented Surface |
|
 Search the VIAS Library | Index
|
  |
Oriented Surface
Before stating the definition we motivate it with a fluid flow interpretation. Remember that in the plane the line integral
is equal to the flux, or net rate of fluid flow across the curve C in the direction of the normal vector N. Consider a fluid flow field F(x, y, z) = Pi + Qj + Rk and a surface S in space. Call one side of S positive and the other side negative, and at each point of S let N be the unit normal vector on the positive side of S. The surface integral
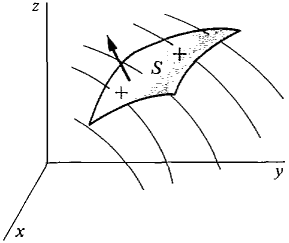
will be the flux, or net rate of fluid flow across the surface S from the negative to the positive side (Figure 13.5.5).
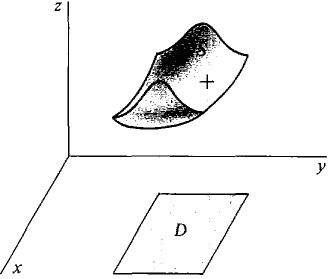
Figure 13.5.5 With this interpretation in mind we shall define the surface integral and then justify the definition. First we need the notion of an oriented surface. DEFINITION An oriented surface S is a smooth surface z = g(x, y) over a plane region D with a piecewise smooth boundary, together with an orientation that designates one side of the surface as positive and the other side as negative. (See Figure 13.5.6.)
Figure 13.5.6: An oriented surface
|
|
| Home Vector Calculus Surface Area and Surface Integrals Oriented Surface |
|
Last Update: 2006-11-22