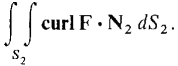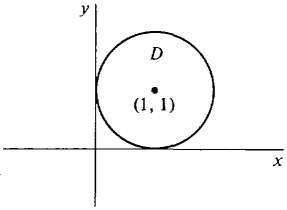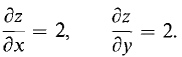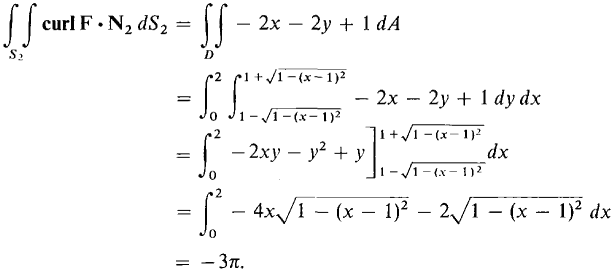Example 2

EXAMPLE 2

Let S₁ be the portion of the plane

z = 2x + 2y - 1

and S₂ the portion of the paraboloid

z = x² + y²

bounded by the curve where the plane and paraboloid intersect. Orient both surfaces with the top side positive, so they have the same boundary

C = ∂S₁ = ∂S₂.

Let

F(x, y, z) = zi + xj + yk.

Evaluate the integrals

(a)

(b)

(c)

By Stokes' Theorem, all three answers are equal, but we compute them separately as a check.

The regions are drawn in Figure 13.6.5. First we find the plane region D over which S₁ and S₂ are defined. The two surfaces intersect at

2x + 2y - 1 = x² + y², (x - 1)² + (y - 1)² = 1.

Figure 13.6.5

So D is the unit circle with center at (1,1) shown in Figure 13.6.6; that is,

0 ≤ x ≤ 2,

Figure 13.6.6

Next we compute curl F.

(a)    On the surface z = 2x + 2y - 1,

Thus

(b)    On the surface z = x² + y²,

Thus

(c)    The boundary curve C = ∂S_l = ∂S₂ is a space curve on the plane z = 2x + 2v - 1 and over the circle

(x - 1)² + (y - 1)² = 1.

Thus C has the parametric equations

x = 1 + cos θ, y = 1 + sin θ, z = 2 cos θ + 2 sin θ + 3, 0 ≤ 0 ≤ 2π.

Then

dx = -sin θ dθ, dy = cos θ dθ,

dz = (-2 sin θ + 2 cos θ)dθ.

Notice that (a) was much easier than (b) or (c).