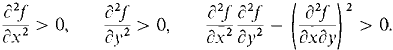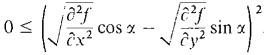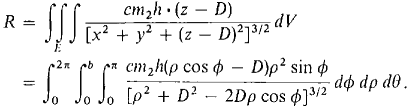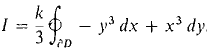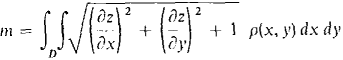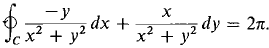| 1 |
Find the derivative of z = cos x + sin y in the direction of the unit vector U = cos αi + sin αj. |
| 2 |
Find grad f and fU if

|
| 3 |
Find grad f and fU if f(x, y) = exy, U = cos αi + sin αj. |
| 4 |
Find the derivative of z = ln (x2 + y2) at the point (-1,1) in the direction of the unit vector U = ai + bj. |
| 5 |
Find a unit vector normal to the surface z = xy at the point (2, 3, 6). |
| 6 |
Evaluate the line integral
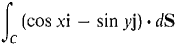
where C is the curve x = t2, y = t3, 0 ≤ t ≤ 1. |
| 7 |
Evaluate the line integral
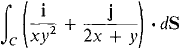
where C is the rectangular curve from (1, 2) to (4, 2) to (4,4). |
| 8 |
Evaluate the line integral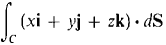
where C is the line x = 2t, y = 3t, z = -t, 0 ≤ t ≤ 1. |
| 9 |
Find the work done by the force F = y2i + x2j acting once counterclockwise around the circle x2 + y2 = 1. |
| 10 |
Find a potential function for y cosh xi + sinh xj. |
| 11 |
Find a potential function for (y ln y + ln x)i + (x ln y + x)j. |
| 12 |
Solve the differential equation (2x - 6x2y + y3)dx + (-2x3 + 3xy2 + 1)dy = 0. |
| 13 |
Solve the differential equation e-y sin x dx + (e~y cos x + 3y) dy. |
| 14 |
Use Green's Theorem to evaluate the line integral

D: π/6 ≤ x ≤ π/3, π/6 ≤ y ≤ π/3. |
| 15 |
Use Green's Theorem to evaluate the line integral

|
| 16 |
Use Green's Theorem to find the area of the region bounded by the parametric curve
x = a cos3 θ, y = a sin3 θ, 0 ≤ θ ≤ 2π. |
| 17 |
Find the area of the part of the surface z = x2 + y which lies over the triangular region 0 ≤ x ≤ l, 0 ≤ y ≤ x. |
| 18 |
Find the area of the part of the surface z = xy which is inside the cylinder x2 + y2 = 4. |
| 19 |
Evaluate the surface integral

where S is the upper half of the sphere x2 + y2 + z2 = 1, oriented with the top side positive. |
| 20 |
Find the curl and divergence of the vector field
F(x,y) = xeyi + ye*]. |
| 21 |
Find the curl and divergence of the vector field
F(x,y,z) = xyzi + xy2z3j + x2yzk. |
| 22 |
Use Gauss' Theorem to evaluate the surface integral

where E is the region x2 + y2 ≤ 1, x2 + y2 ≤ z ≤ 1. |
| 23 |
The gravitational force of a point mass ml acting on another point mass m2 has the direction of the vector D from m2 to m1 and has magnitude proportional to the inverse square of the distance |D|. Thus

where c is constant. Use the Infinite Sum Theorem to show that the gravitational force of an object with density h(x, y, z) in a region E on a point mass m at (a, b, c) is
F = Pi + Qj + Rk,
where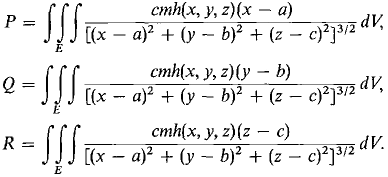 |
| 24 |
Suppose z = f(x,y) is differentiable at (a,b). Prove that the directional derivatives fU(a, b) exist for all U. (See also extra Problem 36 in Chapter 11.) |
| 25 |
Let U = cos αi + sin αj. Suppose that z = f(x, y) has continuous second partial derivatives. Prove that the second directional derivative of f in the direction U is given by
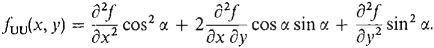
|
| 26 |
Second Derivative Test for two variables. Suppose
(a) f(x, y) has an interior critical point (a, b) in a rectangle D.
(b) Throughout D, 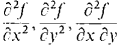 are continuous and are continuous and
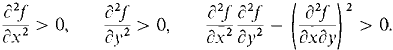
Prove that f has a minimum in D at (a,b). Hint: Use the preceding problem to show that all the second directional derivatives fUU(x,y) are positive so that the surface z = f(x,y) has a minimum in every direction at (a,b). In the case cos α sin α > 0, use the inequality
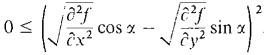
and use a similar inequality when cos α sin α < 0. |
| 27 |
Given a sphere of mass m1 and constant density, and a point mass m2 outside the sphere at distance D from the center. Show that the gravitational force on m2 is the same as it would be if all the mass of the sphere were concentrated at the center. That is, F points toward the center and has magnitude

Hint: For simplicity let the center of the sphere be at the origin and let m2 be at the point (0, 0, D) on the z-axis. Let the sphere have radius b and density h, so
h = m1/volume = 3m1/4πb3, b < D.
By symmetry the i and j components of the force are zero. Use spherical coordinates to find the k component,
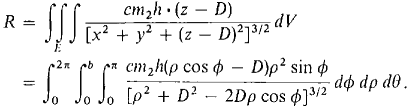
|
| 28 |
A region D in the plane has a piecewise smooth boundary ∂D and area A. Use Green's Theorem to show that an object with constant density k in D has center of mass

|
| 29 |
Show that the object in the preceding exercise has moment of inertia about the origin
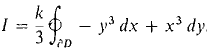
|
| 30 |
Use the Infinite Sum Theorem to show that the mass of a film of density p(x, y) per unit area on a surface z = f(x, y), (x, y) in D, is
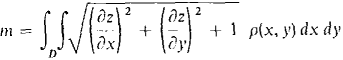
|
| 31 |
Show that the volume of a region E is equal to the surface integral

|
| 32 |
Show that the gravity force field of a mass m at the origin,

is irrotational (except at the origin). Use Stokes' Theorem to show that

where S is any oriented surface not containing the origin. |
| 33 |
Show that for any smooth closed curve C around the origin,
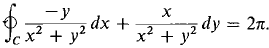
Assume for simplicity that C has the parametric equation
C: r = f(0), 0 ≤ d ≤ 2π where 0 < f(0), f(0) = f(2π). |


 Vector Calculus
Vector Calculus  Extra Problems for Chapter 13
Extra Problems for Chapter 13





 Vector Calculus
Vector Calculus  Extra Problems for Chapter 13
Extra Problems for Chapter 13


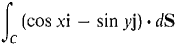
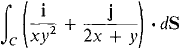
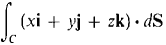





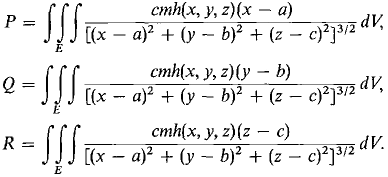
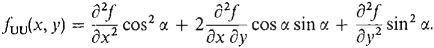
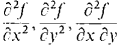 are continuous and
are continuous and