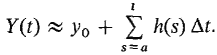| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Differential Equations Differential Equations  Existence and Approximation of Solutions Existence and Approximation of Solutions  Existence Theorem Existence Theorem |
|






|
|
Existence Theorem
Let Δt be positive infinitesimal and let Y(t) be the Euler approximation of the initial value problem (1) y' = f(t, y), y(a) = y0
Figure 14.4.3 with increment Δt. Let b be a real number greater than a, and suppose that Y(t) is finite for all t between a and b. Then for real numbers t in the interval [a, b], the function y(t) given by y(t) = st(Y(t)) is a solution of the initial value problem (1). Discussion The theorem shows that the initial value problem (1) has a solution as long as Y(t) remains finite. The solution is found by taking the standard part of Y(t). When Y(t) becomes infinite, we say that an explosion occurs (see Example 2 in Section 14.1 and Example 3 in this section). PROOF OF THE EXISTENCE THEOREM At t = a, y(a) = st(Y(a)) = y0. Let M be the largest value of |f(t, Y(t))| for t, a partition point between a and b. Then M is finite. Since Y(t) never changes by more than MΔt from one partition point to the next, we always have |Y(t) - Y(s)| ≤ M|t - s|. Taking standard parts, we see that for real s and t in the interval [a, b], |y(t) - y(s)| ≤ M |t - s|. By the Transfer Principle, this also holds for all hyperreal s and t between a and b. Then for any a ≤ t ≤ b, 7(t) ≈ Y(st(t)) ≈ y(st(t)) ≈ y(t) and hence, because f(t, z) is continuous in z, f(t, Y(t)) ≈ f(t, y(t)). Let h(t) be the real function h(t) = f(t, y(t)). Since Y is an Euler approximation,
for each real point t between a and b. But h(s) = f(s, y(s)) ≈ f(s, Y(s)), so
This is just the Riemann sum of h. Taking standard parts, we get the integral of h:
Finally, by the Fundamental Theorem of Calculus, y'(t) = h(t) = f(t, y(t)). Thus y(t) is a solution of (1) as required. To apply the Existence Theorem, we need a way of checking that Y(t) is finite. Here is a convenient criterion. LEMMA Let Y(t) be an Euler approximation of the initial value problem (1) with infinitesimal Δt, and let M and b be finite. (i) If |f(t, y)| ≤ M for all a ≤ t ≤ b and all y, then Y(t) is finite for all a ≤ t ≤b. (ii) If |f(t, y)| ≤ M for all a ≤ t ≤ b and all y within M · (t - a) of y0, then Y(t) is finite for all a ≤ t ≤ b. PROOF (i) Since Y(t) cannot change by more than M Δt from one partition point to the next, we have |Y(t) - y0| ≤ M · (t - a) ≤ M · (b - a). M · (b - a) is finite, so Y(t) is finite. The proof of (ii) is similar. Discussion The lemma is illustrated in Figure 14.4.4. Choose a positive real number M. Part (i) of the lemma says that if f(t, y) is between -M and M, everywhere in the vertical strip between t = a and t = b, then Y(t) is finite for a ≤ t ≤ b. Part (ii) of the lemma says that if f(t, y) is between -M and M, everywhere in the shaded triangle, then Y(t) is finite for a ≤ t ≤ b. Part (ii) is stronger because the shaded triangle is a subset of the vertical strip. The proof shows that Y(t) stays within the shaded rectangle for a ≤ t ≤ b. The lemma and the Existence Theorem combined show that if we can find an M such that f(t, y) is continuous and f(t, y) is between -M and M everywhere in the shaded triangle, then the initial value problem (1) has a solution y(t) for a ≤ t ≤ b. The proof also shows that the solution y(t) is within the shaded triangle for a ≤ t ≤ b.
Figure 14.4.4
|
|
Home  Differential Equations Differential Equations  Existence and Approximation of Solutions Existence and Approximation of Solutions  Existence Theorem Existence Theorem |
|
Last Update: 2010-11-25