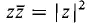Example 3

Find the roots of the polynomial z² + z + 2 in the complex number system.

It is often useful to represent a complex number in polar form. A point (x, y) in the plane has polar coordinates (r, θ) where x = r cos θ, y = r sin θ. The complex number x + iy may be written in the polar form

x + iy = r(cos θ + i sin θ).

The coordinates r and θ can always be chosen so that r ≥ 0 and -π < θ ≤ π. The number r, which is the distance of the point (x, y) from the origin, is the absolute value of the complex number x + iy:

r= |x + iy| = (x² +y²)^1/2.

The formula (1) for the product of a complex number and its conjugate may now be written in the short form

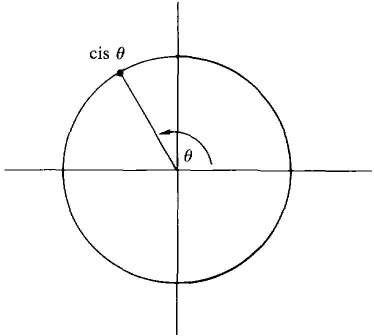
The real number θ is an angle in radians and is called the argument of x + iy. The argument can be computed by using the formula

tan (y/x) = θ,

and then choosing θ in the correct quadrant. The polar form of a complex number is illustrated in Figure 14.5.2. This figure is sometimes called the Argand diagram of the complex number. The complex number with absolute value one and argument θ is sometimes called cis θ:

cis θ = cos θ + i sin θ.

Figure 14.5.2

In Figure 14.5.3, we see that in the complex plane, cis θ is on the unit circle at an angle θ counterclockwise from the x-axis. Using the symbol cis θ, the polar form can be written

x + iy = r cis θ.

Figure 14.5.3