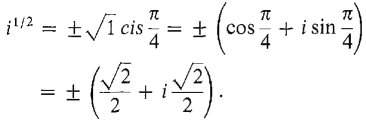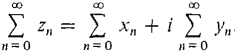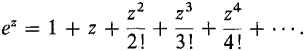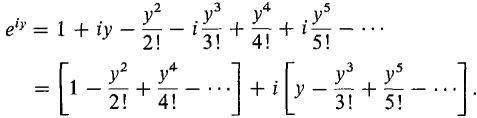Example 6

Find the square roots of i.

By the computation in Example 3, the polar form of i is i = cis (π/2).

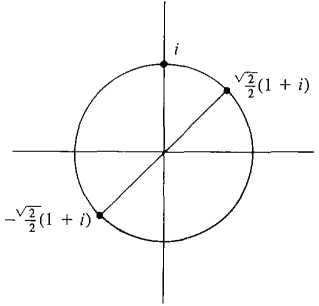
The two square roots of i are shown in Figure 14.5.4.

Figure 14.5.4

We now turn to complex exponents, which are useful in the study of differential equations. In order to give a meaning to an exponent e², we consider infinite series of complex numbers. The sum of an infinite series of complex numbers is defined by summing the real and imaginary parts separately. If z_n = x_n + iy_n, and the series ∑x_n and ∑y_n both converge, the sum of the series ∑z_n is defined by the formula

In Chapter 9, we found that for real numbers z the exponent e^z is given by the power series

When z is a complex number, this formula is taken as the definition of e^z. It can be shown that the power series converges for every z and that the exponential rule e^u+z = e^u e^z holds for complex exponents. In the case that z is a purely imaginary number z = iy, the power series takes the form

Using the power series for cos y and sin y, we obtain Euler's Formula:

e^iy = cos y + i sin y = cis y.

When z is a complex number z = x + iy, the exponent e^z is given by the formula g^{x + iy} = e^x e^iy = e^x(cos y + i sin y).