| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Differential Equations Differential Equations  Complex Numbers Complex Numbers  Problems Problems |
|






|
|
Problems
In Problems 1-6, put the complex number in the form a + ib.
In Problems 7-12, find the roots of the given equation.
In Problems 13-18, put the complex number into the polar form r cis θ.
In Problems 19-24, use the polar form to simplify the given expression.
In Problems 25-28, compute both square roots of the given complex number using the polar form.
In Problems 29-32, put the given exponent in the form a + ib.
In Problems 33-36, find the derivative.
In Problems 37-40, find the general solution of the complex differential equation.
In Problems 41-44, solve the given complex initial value problem.
46 Prove that the conjugate of a complex number r cis θ is r cis (-θ). 47 Prove that for any nonzero complex number z, 48 Prove that for any two complex numbers u and z, the sum of the conjugates of u and z is equal to the conjugate of the sum of u and z, and similarly for products. In symbols,
49 Prove that for any two complex numbers u and z,
50 Use De Moivre's Formula with n = 2, cos (2θ) + i sin (2θ) = (cos θ + i sin θ)2, to obtain expressions for cos (2θ) and sin (2θ) in terms of cos θ and sin θ. 51 Use De Moivre's Formula with n = 3, cos (3θ) + i sin (3θ) = (cos θ + i sin θ)3, to obtain expressions for cos (3θ) and sin (3θ) in terms of cos θ and sin θ. 52 Find the solution of the initial value problem z' + (a + ib)z = 0, z(0) = ec+id where a, b, c, and d are real numbers. 53 Show that every solution of the differential equation z' + ibz = 0 has constant absolute value (where b is a real number).
|
|
Home  Differential Equations Differential Equations  Complex Numbers Complex Numbers  Problems Problems |
|
Last Update: 2006-11-25











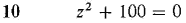
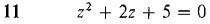









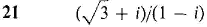
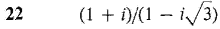
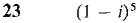











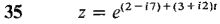

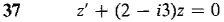

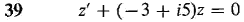

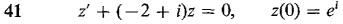

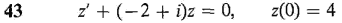


 , where θ is the argument of z.
, where θ is the argument of z.
