| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Differential Equations Differential Equations  Second Order Homogeneous Linear Equations Second Order Homogeneous Linear Equations  Graphs of Solutions of Second Order Homogeneous Linear Equations Graphs of Solutions of Second Order Homogeneous Linear Equations |
|






|
|
Graphs of Solutions of Second Order Homogeneous Linear Equations
Our next topic is graphs of solutions of second order homogeneous linear equations. Several cases arise, including simple, damped, and overdamped oscillations. Consider the second order homogeneous linear differential equation (1) ay" + by' + c = 0. We shall concentrate on the case that a > 0, b ≥ 0, c > 0. (We can always make a positive by changing all the signs if a is negative. The cases with negative b or c are considered in the problem set at the end of the section.) The equation has the characteristic polynomial az2 + bz + c. Let d be the discriminant of this polynomial, d = b2 - 4ac. Simple Oscillation This type of solution arises when b = 0. Since a and c are assumed to be positive, the discriminant d = -4ac is negative, and the characteristic polynomial has two purely imaginary roots, ± iβ. The general solution of equation (1) is y(t) = A cos (βt) + B sin (βt). It is helpful to put this equation in a different form. The point (A, B) is on the circle with center at the origin and radius C = (A2 + B2)1/2. There is thus an angle θ for which A = C cos θ, B = C sin θ, as in Figure 14.6.4. The angle θ can be computed as follows:
Figure 14.6.4 Using the formula for the cosine of the difference of two angles, cos (φ - θ) = cos (φ) cos (θ) + sin (φ) sin (θ), we find that y(t) = C cos (βt) cos (θ) + C sin (βt) sin (θ) = C cos (βt - θ), so that y(t) = C cos (βt - θ). The number C is called the amplitude, because the cosine curve oscillates between C and - C. The number β is called the frequency, because the curve will complete β cycles each 2π units of time. The number 2π/β is called the period, because each cycle is 2π/β units long. The angle θ is called the phase shift. Thus the graph of each particular solution is a cosine wave with amplitude C, period 2π/β, and phase shift θ, as illustrated in Figure 14.6.5.
Figure 14.6.5 Damped Oscillation This case arises when b is positive and the discriminant is negative, b > 0 and d < 0. Here b is in the range 0 < b < √(4ac). The roots of the characteristic polynomial are complex conjugates, a + iβ. The real part a = -b/2a is negative. The general solution is y(t) = eαt(A cos (βt) + B sin (βt)]. Each particular solution oscillates with period 2π/β, but the amplitude dies down exponentially as t increases, as in Figure 14.6.6.
Figure 14.6.6 As in the case of simple oscillation, the solution may be written in the form y(i) = eαtC cos (βt - θ), where C = (A2 + B2)1/2 and θ is a constant angle. The amplitude at time t will then be eαtC, which is decreasing because α is negative. Critical Damping This case arises when b is positive and the discriminant is zero, so that r = -b/2a. The general solution is y(t) = Aert + Btert. Each particular solution will approach 0 as t approaches infinity and will never complete one oscillation. A solution can cross the x-axis once, but never more than once. See Figure 14.6.7.
Figure 14.6.7 Overdamping This case arises when b is positive and the discriminant is positive, so that b > √(4ac). The characteristic polynomial has two real roots, r and s. Since a, b, and c are positive, the characteristic polynomial cannot have any positive or zero roots. Therefore both roots r and s are negative. The general solution is y(t) = Aert + Best. Again, each particular solution approaches zero as t approaches infinity and will never complete one oscillation, as in Figure 14.6.7. The differential equations of this section provide simple models for a variety of physical systems that oscillate, such as mass-spring systems and electrical networks. When a horizontal spring of natural length L is compressed a distance x, it exerts a force of approximately F = -kx. k is called the spring constant and depends on the particular spring. The negative sign indicates that the force is in the opposite direction from x, as in Figure 14.6.8. A mass m is attached to the end of the spring. From Newton's Law, F = ma = mx", we obtain a second order differential equation for the position x(t), mx" = -kx, or mx" + kx = 0.
Figure 14.6.8 Both constants k and m are positive, and the solution is the simple oscillation x(t) = A cos (βt) + B sin (βt) where β = (k/m)1/2. A mass-spring system immersed in oil (such as an automobile shock absorber) is subject to a damping force bx'(t), which is proportional to the velocity x'(t) but in the opposite direction. This additional force will slow down the motion of the spring and lead to a damped oscillation. The force is approximately F = -bx' - kx and thus satisfies the differential equation mx" + bx' + kx = 0. When the damping constant b is between 0 and (4mk)1/2, the solution will be a damped oscillation. The greater the value of b, the more quickly the oscillation will be damped down. When b is equal to (4mk)1/2, the solution will be critically damped; when b is greater than (4mk)1/2, the solution will be overdamped.
|
|
Home  Differential Equations Differential Equations  Second Order Homogeneous Linear Equations Second Order Homogeneous Linear Equations  Graphs of Solutions of Second Order Homogeneous Linear Equations Graphs of Solutions of Second Order Homogeneous Linear Equations |
|
Last Update: 2006-11-25






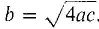 The characteristic polynomial has one negative real root,
The characteristic polynomial has one negative real root,
