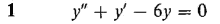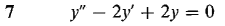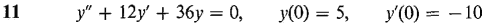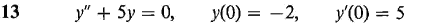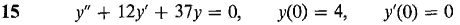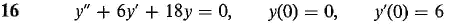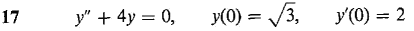The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Differential Equations Second Order Homogeneous Linear Equations Problems
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Problems

In Problems 1-8, find the general solution of the given differential equation.

14_differential_equations-205.gif

14_differential_equations-206.gif

14_differential_equations-207.gif

14_differential_equations-208.gif

14_differential_equations-209.gif

14_differential_equations-210.gif

14_differential_equations-211.gif

14_differential_equations-212.gif

In Problems 9-16, find the particular solution of the initial value problem.

14_differential_equations-213.gif

14_differential_equations-214.gif

14_differential_equations-215.gif

14_differential_equations-216.gif

14_differential_equations-217.gif

14_differential_equations-218.gif

14_differential_equations-219.gif

14_differential_equations-220.gif

In Problems 17-20, solve the initial value problem and find the amplitude, frequency, and phase shift of the solution.

14_differential_equations-221.gif

14_differential_equations-222.gif

14_differential_equations-223.gif

14_differential_equations-224.gif

21            A mass-spring system mx" + bx' + kx = 0 has spring constant k = 29, damping constant b = 4, and mass m = 1. At time t = 0, the position is x(0) = 2 and the velocity is x'(0) = 1. Find the position x(t) as a function of time.

22            A mass-spring system mx" + bx' + kx = 0 has spring constant k = 24, damping constant b = 12, and mass m = 3. At time t = 0, the position is x(0) = 0 and the velocity is x'(0) = -1. Find the position x(t) as a function of time.

23            Show that if y(t) is a solution of a differential equation ay" + by' + cy = 0, such that y(t0) = 0 and y'(t0) = 0 at some time t0, then y(t) = 0 for all t.

24            In the differential equation ay" + by' + cy = 0, suppose that a is positive and c is negative. Show that the characteristic equation has one positive real root and one negative real root, so that the general solution has the form y = Aert + Best where r is positive and s is negative.

25            In the differential equation ay" + by' + cy - 0, suppose that a and c are positive and b is negative. Show that there are three cases for the general solution, depending on the sign of the discriminant d:

Case 1

If d is positive, the general solution has the form y = Aert + Best where r and s are positive.

Case 2

If d is zero, the general solution has the form y = Aert + Btert where r is positive.

Case 3

If d is negative, the general solution has the form y = eαt[A cos (βt) + B sin (βt)] where α is positive, so that the graph is an oscillation whose amplitude is increasing instead of decreasing.

Home Differential Equations Second Order Homogeneous Linear Equations Problems

Last Update: 2006-11-25