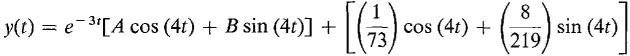Example 6

Find a particular solution of the differential equation

y" + 6y' + 25y = cos (4t).

The characteristic polynomial z² + 6z + 25 has roots - 3 ± i4. Since i4 itself is not a root, the proper guess is

y(t) = K cos (4t) + L sin (4t).

Both a cosine term and a sine term are required, because the derivative of a sine is a cosine. Compute the first two derivatives of y(t).

y'(t) = -4K sin (4t) + 4L cos (4t),

y"(t) = -16K cos (4t) - 16L sin (4t).

Now substitute into the original differential equation.

cos (4t)

= [- 16K cos (4t) - 16L sin (4t)] + 6[-4K sin (4t) + 4L cos (4t)] + 25[K cos (4t) + L sin (4t)]

= (- 16K + 24L + 25K) cos (4t) + (- 16L - 24K + 25L) sin (4t).

Both the sin (4t) coefficients and the cos (4t) coefficients must be the same on both sides of the equation. Thus we have two equations in the two unknowns K and L.

sin (4t) terms:

0 = -24K + 9L.

cos (4t) terms:

1 = 9K + 24L.

Solve for K and L.

The required particular solution is

In Example 6, the particular solution is a simple oscillation, while the general solution of the corresponding homogeneous equation is a damped oscillation. The general solution is their sum:

The first term, e^-3t[A cos (4t) + B sin (4t)], approaches zero as t → ∞ and is called the transient part of the solution. The second term, [(1/73) cos (4t) + (8/219) sin (4f)], is called the steady part of the solution. The constants A and B, which depend on the initial conditions, appear only in the transient part and not in the steady state part of the solution. No matter what the initial conditions are, every particular solution will approach the steady state part of the solution as t → ∞. The effect of the initial conditions dies out as t → ∞.

The same thing happens in any mass-spring system with damping where the forcing term is a simple oscillation. Let us consider a mass-spring system

(5)

my" + by' + ky = cos (ωt),

where m, b, and k are positive and the forcing term cos (ωt) has frequency ω. A particular solution can be found of the form

K cos (ωt) + L sin (ωt).

The constants K and L can be computed as in Example 6. The general solution of equation (5) is

y(t) = e^-αt[A cos (βt) + B sin (βt)] + [K cos (ωt) + L sin (ωt)].

As in Example 6, the first term approaches 0 as t → ∞ and is called the transient part of the solution, and the second term is called the steady state part of the solution. Again, every particular solution of the mass-spring system will approach the steady state part of the solution as t → ∞.