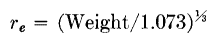Intermittent Ratings

It often happens that electronic equipment is operated for repeated short lengths of time, between which the power is off. In such cases the average power determines the heating and size. Transformers operating intermittently can be built smaller than if they were operated continuously at full rating.

Intermittent operation affects size only if the "on" periods are short compared to the thermal time constant of the transformer; that is, small transformers have less heat storage capacity and hence rise to final temperature more quickly than do large ones. It is important, therefore, to know the relation between size and thermal time constant, or the time that would be required to bring a transformer to 63 per cent of the temperature to which it would finally rise if the power were applied continuously.

The exact determination of temperature rise time in objects such as transformers, having irregular shapes and non-homogeneous materials, has not yet been attempted. Even in simple shapes of homogeneous material, and after further simplifying assumptions have been made, the solution is too complicated ⁽¹⁾ for rapid calculation. However, under certain conditions, a spherical object can be shown to cool according to the simple law: ⁽²⁾

[28]

where

θ = temperature above ambient at any instant t
θ₀ = initial temperature above ambient
E = emissivity in calories per second per centigrade degree per square centimeter
p = density of material
c = specific heat of material
r = radius of sphere
ε = 2.718.

The conditions involved in this formula are that the sphere is so small or the cooling so slow that the temperature at any time is sensibly uniform throughout the whole volume. Mathematically, this is fulfilled when the expression Er/k (where k is the thermal conductivity of the material) is small compared to unity. Knowing the various properties of the transformer material, we can tell (1) whether the required conditions are met, and (2) what the thermal time constant is. The latter is arrived at by the relation

[29]

where r_e is the radius of the equivalent sphere.

In order to convert the non-homogeneous transformer into a homogeneous sphere the average product of density and specific heat pc is found. Figures on widely different transformers show a variation from 0.862 to 0.879 in this product; hence an average value of 0.87 can be taken, with only 1 per cent deviation in any individual case.

Since the densities of iron and copper do not differ greatly, and insulation brings the coil density closer to that of iron, it may be further assumed that the transformer has material of uniform density 7.8 throughout. The equivalent spherical radius can then be found from

[30]

where r_e is in inches and weight is in pounds. The time constant is plotted from equations 29 and 30 in terms of weight in Fig. 46.

Fig. 46. Transformer time constant, or time required to reach 63 per cent of final temperature.

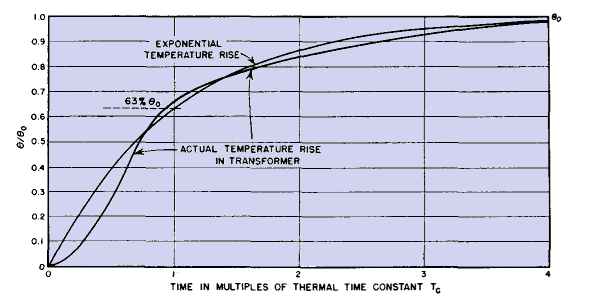
The condition that Er/k be small compared to unity is approximated by assuming that fc is the conductivity of iron-a safe assumption, because the conductivity of copper is 7 to 10 times that of iron. A transformer weighing as much as 60 lb has r_e = 5.45 in., E = 0.00028 cal per sec per sq cm/°C, and k = 0.11. Changing r_e to metric units gives Er/k = (0.00028 · 5.45 · 2.54)/0.11 = 0.34, which is small enough to meet the necessary condition of equation 28.

It will be noticed that equation 28 is a law for cooling, not temperature rise. But if the source of heat is steady (as it nearly is) the equation can be inverted to the form θ₀ - θ for temperature rise, and θ_o becomes the final temperature.

Temperature rise of a typical transformer is shown in Fig. 47, together with the exponential law which is θ₀ - θ, where θ is the temperature of equation 28.

Fig. 47. Transformer temperature rise time.

The actual rise is less at first than that of the foregoing simplified theory, then more rapid, and with a more pronounced "knee." The 63 per cent of final temperature is reached in about 70 per cent of the theoretical time constant t_c for transformers weighing between 5 and 200 lb. This average correction factor is included in Fig. 46 also.

If a transformer is operated for a short time and then allowed to cool to room temperature before operating again, the temperature rise can be found from Figs. 46 and 47. As an example, suppose that the continuously operated final coil temperature rise is 100 centigrade degrees, the total weight is 5 lb, and operating duty is infrequent periods of 2 hr. From Fig. 46, the transformer has a thermal time constant of 0.85 hr. This corresponds to t_c = 1 in Fig. 47. Two hours are therefore 2 / 0.85 = 2.35 times t_c, and the transformer rises to 90 per cent of final temperature, or a coil temperature rise of 90 centigrade degrees, in 2 hr.

If, on the other hand, the transformer has regular off and on intervals, the average watts dissipated over a long period of time govern the temperature rise. A transformer is never so small that it heats up more in the first operating interval than at the end of many intervals. From equation 30 can be found a relation between weight, losses, and final temperature rise. For, since heat is dissipated at 0.008 watt per sq in./°C rise, and the area A_s of the equivalent sphere is 4πr_e⁽²⁾,

[31]

where θ_o is the final temperature rise in centigrade degrees. This equation is subject to the same approximations as equation 28; test results show that it is most reliable for transformers weighing 20 lb or more, with 55°C temperature rise at 40°C ambient.

(1)	See The Mathematical Theory of Heat Conduction, by L. R. Ingersoll and O. J. Zobel, Ginn and Co., Boston, 1913, p. 142.
(2)	Ingersoll and Zobel, op. cit., p. 143.