VIAS Encyclopedia provides a collection of tables and definitions commonly needed in science and engineering.

Home Computer Science Huffman Encoding
See also: ASCII, ANSI and EBCDIC Encoding 
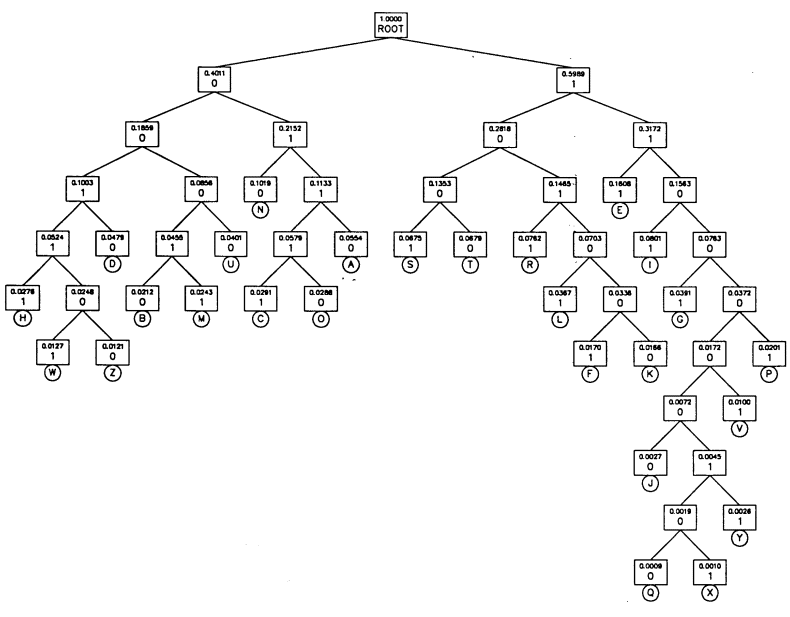
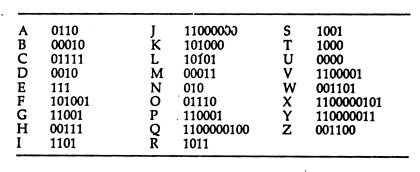
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter

Huffman Coding

Huffman coding, which has been developed by David A. Huffman in 1952, is an entropy encoding algorithm used for lossless data compression. The term refers to the use of a variable-length code table for encoding a source symbol (such as a character in a file) where the variable-length code table has been derived in a particular way based on the estimated probability of occurrence for each possible value of the source symbol.

Huffman coding uses a specific method for choosing the representation for each symbol, resulting in a prefix-free code (that is, the bit string representing some particular symbol is never a prefix of the bit string representing any other symbol) that expresses the most common characters using shorter strings of bits than are used for less common source symbols. Huffman was able to design the most efficient compression method of this type: no other mapping of individual source symbols to unique strings of bits will produce a smaller average output size when the actual symbol frequencies agree with those used to create the code.

Note: Huffman coding is such a widespread method for creating prefix-free codes that the term "Huffman code" is widely used as a synonym for "prefix-free code" even when such a code was not produced by Huffman's algorithm.

Assertions of the optimality of Huffman coding should be phrased carefully, because its optimality can sometimes accidentally be over-stated. For example, arithmetic coding ordinarily has better compression capability, because it does not require the use of an integer number of bits for encoding each source symbol. LZW coding can also often be more efficient, particularly when the input symbols are not independently distributed. The efficiency of Huffman coding also depends heavily on having a good estimate of the true probability of the value of each input symbol.

Following is an example how to construct a Huffman code. Suppose you have to encode a text which contains only characters with the following frequencies of occurence:

In order to construct the binary tree from which the Huffman coding can be deducted, one has to proceed as follows:
  1. Initially, each character forms a (unconnected) node which is marked by the probability of occurence of the character.
  2. Find the two nodes which show the lowest probability to occur and connect them by a node common to both.
  3. Assign a probability to the new node which is the sum of the two initial nodes.
  4. Repeat from step 2 until all nodes have been connected.
The final node (or root of the tree) should show a probability of 1.0 (apart from rounding errors).

In order to assign the Huffman codes to the letters of our text, we simply go along the binary tree from the root element to the leaf of a particular character, recording all digits (0 or 1) of all nodes along the path.

As you can easily see, the Huffman encoding uses only a few bits for encoding characters with high frequencies, while characters with low frequencies (i.e. an X) are ecoded by many bits.

Decoding a Huffman-encoded bit stream

The decoding procedure is deceptively simple. Starting with the first bit in the stream, one uses successive bits from the stream to determine whether to go left or right in the decoding tree. When we reach a leaf of the tree, we've decoded a character, so we place that character into the (uncompressed) output stream. The next bit in the input stream is the first bit of the next character.

Home Computer Science Huffman Encoding

Last Update: 2005-10-04