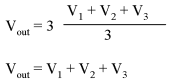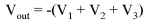| The ebook FEEE - Fundamentals of Electrical Engineering and Electronics is based on material originally written by T.R. Kuphaldt and various co-authors. For more information please read the copyright pages. |

|

Home  Semiconductors Semiconductors  Operational Amplifiers Operational Amplifiers  Averager and summer circuits Averager and summer circuits |
|||






|
|||
|
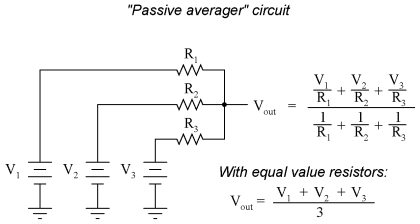
Averager and summer circuitsIf we take three equal resistors and connect one end of each to a common point, then apply three input voltages (one to each of the resistors' free ends), the voltage seen at the common point will be the mathematical average of the three.
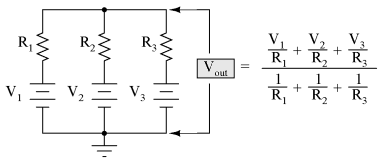
This circuit is really nothing more than a practical application of Millman's Theorem:
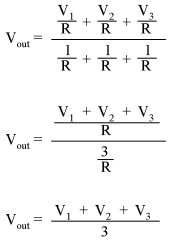
This circuit is commonly known as a passive averager, because it generates an average voltage with non-amplifying components. Passive simply means that it is an unamplified circuit. The large equation to the right of the averager circuit comes from Millman's Theorem, which describes the voltage produced by multiple voltage sources connected together through individual resistances. Since the three resistors in the averager circuit are equal to each other, we can simplify Millman's formula by writing R1, R2, and R3 simply as R (one, equal resistance instead of three individual resistances):
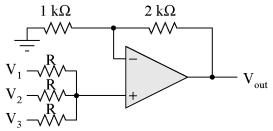
If we take a passive averager and use it to connect three input voltages into an op-amp amplifier circuit with a gain of 3, we can turn this averaging function into an addition function. The result is called a noninverting summer circuit:
With a voltage divider composed of a 2 kΩ / 1 kΩ combination, the noninverting amplifier circuit will have a voltage gain of 3. By taking the voltage from the passive averager, which is the sum of V1, V2, and V3 divided by 3, and multiplying that average by 3, we arrive at an output voltage equal to the sum of V1, V2, and V3:
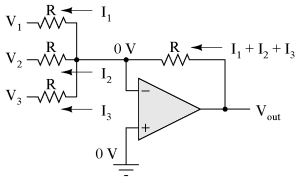
Much the same can be done with an inverting op-amp amplifier, using a passive averager as part of the voltage divider feedback circuit. The result is called an inverting summer circuit:
Now, with the right-hand sides of the three averaging resistors connected to the virtual ground point of the op-amp's inverting input, Millman's Theorem no longer directly applies as it did before. The voltage at the virtual ground is now held at 0 volts by the op-amp's negative feedback, whereas before it was free to float to the average value of V1, V2, and V3. However, with all resistor values equal to each other, the currents through each of the three resistors will be proportional to their respective input voltages. Since those three currents will add at the virtual ground node, the algebraic sum of those currents through the feedback resistor will produce a voltage at Vout equal to V1 + V2 + V3, except with reversed polarity. The reversal in polarity is what makes this circuit an inverting summer:
Summer (adder) circuits are quite useful in analog computer design, just as multiplier and divider circuits would be. Again, it is the extremely high differential gain of the op-amp which allows us to build these useful circuits with a bare minimum of components.
|
|||
Home  Semiconductors Semiconductors  Operational Amplifiers Operational Amplifiers  Averager and summer circuits Averager and summer circuits |
|||
Last Update: 2010-12-01