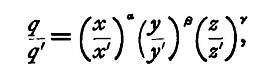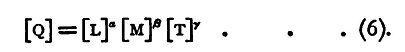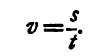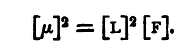Dimensional Equations

We have already pointed out that there are more than one absolute system of units in use by physicists. They are deduced in accordance with the same principles, but are based on different values assigned to the fundamental units. It becomes, therefore, of importance to determine the factor by which a quantity measured in terms of a unit belonging to one system must be multiplied, in order to express it in terms of the unit belonging to another system. Since the systems are absolute systems, certain variation equations become actual equalities; and since the two systems adopt the same principles, the corresponding equations will have the constant k equal to unity for each system. Thus, if we take the equation (1) (p. 14) as a type of one of these equations, we have the relation between the numerical measures

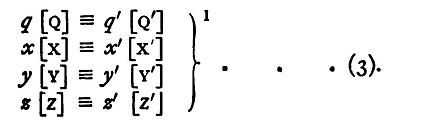
holding simultaneously for both systems.

Or, if q, x, y, z, be the numerical measures of any quantities on the one absolute system; q', x', y', z', the numerical measures of the same actual quantities on the other system,

then

and

Now, following the usual notation, let [Q], [X], [Y], [Z] be the concrete units for the measurement of the quantities on the former, which we will call the old, system, [Q'], [X'], [Y'], [Z'] the concrete units for their measurement on the new system.

Then, since we are measuring the same actual quantities,

In these we may see clearly the expression of the well-known law, that if the unit in which a quantity is measured be changed, the ratio of the numerical measures of the same quantity for the two units is the inverse ratio of the units.

From equations (1) and (2) we get

and substituting from (3).

Thus, if ξ, η, ζ be the ratio of the new units [X'], [Y'], [Z'] to the old units [X], [Y], [Z] respectively, then the ratio ρ of the new unit [Q'] to the old unit [Q] is equal to ξ^α η^β ζ^γ and the ratio of the new numerical measure to the old is the reciprocal of this.

Thus

The equation (4), which expresses the relation between the ratios in which the units are changed, is of the same form as (1), the original expression of the physical law. So that whenever we have a physical law thus expressed, we get at once a relation between the ratios in which the units are changed. We may, to avoid multiplying notations, write it, if we please, in the following form:

where now [Q], [X], [Y], [Z] no longer stand for concrete units, but for the ratios in which the concrete units are changed. It should be unnecessary to call attention to this, as it is, of course, impossible even to imagine the multiplication of one concrete quantity by another, but the constant use of the identical form may sometimes lead the student to infer that the actual multiplication or division of concrete quantities takes place. If we quite clearly understand that the sentence has no meaning except as an abbreviation, we may express equation (5) in words by saying that the unit of Q is the product of the a power of the unit of x, the β power of the unit of Y, and the γ power of the unit of z; but if there is the least danger of our being taken at our word in expressing ourselves thus, it would be better to say that the ratio in which the unit of Q is changed when the units of x, y, z are changed in the ratios of [x] : 1, [Y] : 1 and [z] : i respectively is equal to the product of the α power of [X], the β power of [Y], and the γ power of [Z].

We thus see that if [X], [Y], [Z] be the ratios of the new units to the old, then equation (5) gives the ratio of the new unit of Q to the old, and the reciprocal is the ratio of the new numerical measure to the old numerical measure.

We may express this concisely, thus: If in the equation (5) we substitute for [X], [Y], [Z] the new units in terms of the old, the result is the factor by which the old unit of Q must be multiplied to give the new unit; if, on the other hand, we substitute for [X], [Y], [Z] the old units in terms of the new, then the result is the factor by which the old numerical measure must be multiplied to give the new numerical measure.

If the units [X], [Y], [Z] be derived units, analogous equations may be obtained, connecting the ratios in which they are changed with those in which the fundamental units are changed, and thus the ratio in which [Q] is changed can be ultimately expressed in terms of the ratios in which the fundamental units are changed.

We thus obtain for every derived unit

[L], [M], [T] representing the ratios in which the fundamental units of length, mass, and time, respectively, are changed.

The equation (6) is called the dimensional equation for [Q], and the indices α, β, γ are called the dimensions of Q with respect to length, mass, and time respectively.

The dimensional equation for any derived unit may thus be deduced from the physical laws by which the unit is defined, namely, those whose expressions are converted from variation equations to equalities by the selection of the unit.

We may thus obtain the dimensional equations which are given in the last column of the table (p. 18). We give here one or two examples.

(1) To find the Dimensional Equation for Velocity. Physical law

or

Hence

(2) To find the Dimensional Equation for Force. Physical law

Hence

but

(3) To find the Dimensional Equation for Strength of Magnetic Pole. Physical law

Hence

But

or

When the dimensional equations for the different units have been obtained, the calculation of the factor for con-version is a very simple matter, following the law given on p. 26. We may recapitulate the law here.

To find the Factor by which to multiply the Numerical Measure of a Quantity to convert it from the old System of Units to the new, substitute for [L] [M] and [T] in the Dimensional Equation the old Units of Length, Mass, and Time respectively, expressed in terms of the new.

We may show this by an example.

To find the Factor for converting the strength of a magnetic pole from C.G.S. to Foot-grain-second Units

Writing in the dimensional equation

we get

or the factor required

That is, a pole whose strength is 5 in C.G.S. units has a strength of 0.1165 foot-grain-second units.

1	The symbol = is used to denote absolute identity, as distinguished from numerical equality.