| Practical Physics is a free textbook on basic laboratory physics. See the editorial for more information.... |

|

Home  Measurement of Mass and Specific Gravity Measurement of Mass and Specific Gravity  The Balance The Balance  Sensitiveness of a Balance Sensitiveness of a Balance |
||






|
||
Sensitiveness of a Balance
Let us suppose that this third condition is satisfied, and that the points A, C, B (fig. 7) represent the points in which the three knife-edges cut a vertical plane at right angles to their edges, and let CA, CB make angles α, α' with a horizontal line through C. [If the balance is in perfect adjustment α=α'.]
Then if we draw the vertical lines B'M, A'N to meet the horizontal through C in M and N, a horizontal line through G' to meet CG in X, and consider the equilibrium of the beam, we have by taking moments about the point C
(Q+w+x)CM = (P+W)CN + K Now
CM = CB'cos(α'-θ) = L(cosα'cosθ+sinα'sinθ) Hence we get
Since θ is very small, we may write tan θ=θ,
This gives us the position in which the balance will rest when the lengths of the arms and masses of the scale pans are known, but not necessarily equal or equally inclined to the horizon; and when a difference x exists between the masses in the scale pans. It is evident that θ may be expressed in pointer scale divisions when the angle subtended at the axis of rotation by one of these divisions is known. DEFINITION. - The number of scale divisions between the position of equilibrium of the pointer when the masses are equal and its position of equilibrium when there is a given small difference between the masses is called the sensitiveness of the balance for that small difference. Thus, if the pointer stand at 100 when the masses are equal and at 67 when there is a difference of 0.001 gramme between the masses, the sensitiveness is 33 per milligramme. We have just obtained a formula by which the sensitiveness can be expressed in terms of the lengths of the arms, &c. Let us now suppose that the balance is in adjustment, i.e.
Hence the angle turned through for a given excess weight x increases proportionally with x, and increases with the length of the arm. Let us consider the denominator of the fraction a little more closely. We see that it is positive or negative according as
Now it can easily be shown that the equation
is the condition that c should be the centre of gravity of the beam and the weights of the scale pans, &c. supposed collected at the extremities of the arms. If this condition were satisfied, the balance would be in equilibrium in any position. If Kh be less than L(2P+2w+x)sin α, tan θ is negative, which shows that there is a position of equilibrium with the centre of gravity of the whole, above the axis; but it is reached by moving the beam in the opposite direction to that in which the excess weight tends to move it: it is therefore a position of unstable equilibrium. We need only then discuss the case in which Kh is > L(2P+2w+x)sinα, i.e. when the centre of gravity of the whole is below the axis of rotation. With the extreme knife-edges above the middle one, a is positive and the denominator is evidently diminished, and thus the sensitiveness increased, as the load w increases; but if the balance be so arranged that α=0, which will be the case when the three knife-edges are in the same plane, we have
or the sensitiveness is independent of the load; if the extreme knife-edges be below the mean, so that α is negative, then the denominator increases with the load w, and consequently the sensitiveness diminishes. Now the load tends to bend the beam a little; hence in practice, the knife-edges are so placed that when half the maximum load is in the scale pans, the beam is bent so that all the knife-edges lie in a plane, and the angle a will be positive for loads less than this and negative for greater loads. Hence, in properly made balances, the sensitiveness is very nearly independent of the load, but it increases slightly up to the mean load, and diminishes slightly from the mean to the maximum load.
|
||
Home  Measurement of Mass and Specific Gravity Measurement of Mass and Specific Gravity  The Balance The Balance  Sensitiveness of a Balance Sensitiveness of a Balance |
||
Last Update: 2011-03-27



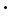 G'X
G'X





