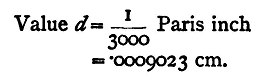Measurement of the Wave-Length of Light

A diffraction grating consists of a number of fine lines ruled at equal distances apart on a plate of glass - a transmission grating; or of speculum metal - a reflexion grating. We will consider the former. If a parallel pencil of homogeneous light fall normally on such a grating, the origin of light being a slit parallel to the lines of the grating, a series of diffracted images of the slit will be seen, and if θ_n be the deviation of the light which forms the n^th image, reckoning from the direction of the incident light, d the distance between the centres of two consecutive lines of the grating, and λ the wave-length, we have

The quantity d is generally taken as known, being determined at the time of ruling the grating. The spectrometer is used to determine θ_n.

The telescope and collimator are adjusted for parallel rays, and the grating placed on the table of the instrument with its lines approximately parallel to the slit. For convenience of adjustment it is best to place it so that its plane is at right angles to the line joining two of the levelling screws. The grating must now be levelled, i.e. adjusted so that its plane is at right angles to the table of the spectrometer. This is done by the method described above for the prism. Then place it with its plane approximately at right angles to the incident light, and examine the diffracted images of the slit. The plane of the grating is at right angles to the line joining two of the levelling screws; the third screw then can be adjusted without altering the angle between the plane of the grating and the table of the spectrometer. Adjust the third screw until the slit appears as distinct as possible; the lines of the grating will then be parallel to the slit.

Turn the table carrying the grating so as to allow the direct light to pass it; adjust the telescope so that the vertical cross-wire bisects the image of the slit seen directly, and read the vernier. This gives us the direct reading. Place the grating with its plane accurately perpendicular to the incident rays, as described above, and turn the telescope to view the diffracted images in turn, taking the corresponding readings of the vernier. The difference between these and the direct reading gives us the deviations θ₁, θ₂, &c. A series of diffracted images will be formed on each side of the direct rays. Turn the telescope to view the second series, and we get another set of values of the deviation θ₁', θ₂', &c. If we had made all our adjustments and observations with absolute accuracy, the corresponding values θ₁, θ₁', &c., would have been the same; as it is their mean will be more accurate than either.

Take the mean and substitute in the formula

We thus obtain a set of values of λ.

If the light be not homogeneous, we get, instead of the separate images of the slit, more or less continuous spectra, crossed it may be, as in the case of the solar spectrum, by dark lines, or consisting, if the incandescent body be gas at a low pressure, of a series of bright lines.

In some cases it is most convenient to place the grating so that the light falls on it at a known angle, φ say. Let ψ be the angle which the diffracted beam makes with the normal to the grating, and θ the deviation for the n^th image, φ and ψ being measured on the same side of the normal, then it may be shown that

and

The case of greatest practical importance is when the deviation is a minimum, and then φ = ψ = θ/2, so that if θ_n denote the minimum deviation for the n^th diffracted image, we have

In the case of a reflexion grating, if φ and ψ denote the angles between the normal and the incident and reflected rays respectively, φ and ψ now being measured on opposite sides of the normal, the formula becomes

and if θ be the deviation

If the value of d be unknown, it may be possible to find it with a microscope of high power and a micrometer eyepiece. A better method is to use the grating to measure θ_n for light of a known wave-length. Then in the formula, nλ = dsinθ_n we know λ, n, and θ_n, and can therefore determine d.

Experiment. - Determine by means of the given grating the wave-length of the given homogeneous light.

Values of deviations, each the mean of three observations:

(1)	See Frontispiece, figs. 5 and 6.