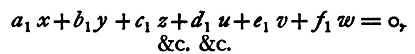The Colour Top

The color top consists of a spindle, which can be rapidly rotated by means of a pulley fixed to it, and from this a string or band passes to the driving wheel of some motor.⁽¹⁾ A disc whose edge is graduated in one hundred parts turns with the spindle, and by means of a nut and washer on the end of the spindle, coloured discs can be fixed against this divided circle. From six coloured papers - black, white, red, green, yellow, and. blue - discs of two sizes are prepared and are then slit along a radius from circumference to centre so as to admit of being slipped one over the other. Each has a hole at the centre through which the spindle can pass.

The apparatus is arranged to show that, if any five out of these six discs be taken, a match or colour equation between them is possible. For instance, if yellow be excluded, the other five may be arranged so that a mixture of red, green, and blue is matched against one of black and white. Take, then, the three large discs of these colours and, slipping them one on the other, fix them against the graduated circle. Start the motor and let it rotate rapidly, looking at the discs against a uniform background of some neutral tint. The three colours will then appear blended into one.

Now place the small discs on these; then on rotating the whole, it will be found that the white and black blend into a grey tint. By continual adjustments an arrangement may be found, after repeated trials, such that the colour of the inner circle is exactly the same both in tint and luminosity as that of the outer ring. The quantities of colour exposed may then be read off on the graduated circle, and it will be found that the proportions are somewhat like the following: 79 parts black and 21 white match 29.2 blue, 29.2 green, and 41.6 red.

With the six discs six equations of this kind can be formed leaving out each colour in turn.

But, according to Maxwell's theory of colour, a match can be found between any four colours, either combining them two and two in proper proportions, or one against three. The colour top is not suited to show this, for with it we have another condition to fulfil. The whole circumference of the circles has in each case to be filled up with the discs. The vacant spaces must therefore be filled up with black, which alters the intensity of the resultant tints; but the intensity may be adjusted by altering the sizes of all the coloured sectors proportionately, and hence with any four colours and black a match can be made.

And thus from the theory the six final equations are not independent; for between any four of the variables, the colours, there exists a fixed definite relation. If, then, we take two of the equations, we can by a simple algebraical calculation find the others. A comparison between the equations thus formed and those given directly as the result of the experiments forms a test of the theory; but in practice it is better, in order to insure greater accuracy, to combine all the equations into two, which may then be made the basis of calculation, and from which we may form a second set of six equations necessarily consistent among themselves and agreeing as nearly as is possible with the observations.

A comparison between these two sets gives evidence as to the truth of the theory, or, if we consider this beyond doubt, tests the accuracy of the observations. The six equations referred to are formed from the six found experimentally by the method of least squares. Thus let us denote the colours by the symbols x, y, z, u, v, w, and the quantities of each used by a₁, b₁, c₁, d₁, e₁, f₁ in the first equation, and by the same letters with 2, 3, &c., subscript in the others, and let Σ{x} denote the sum formed by adding together a series of quantities such as x. Our six equations are

And we have to make

a minimum, treating x, y, z, u, v, w as variables. The resulting equations will be the following:

The calculation of the six equations in this manner is a somewhat long and troublesome process, while the numbers actually arrived at will depend greatly on the exact colours of the discs. In a paper on the subject (' Nature,' Jan. 19, 1871), from which the above account is taken, Lord Rayleigh calls attention to the importance of having the discs accurately cut and centred, otherwise on rotation a coloured ring appears between the two uniform tints and gives rise to difficulty.

The results also depend to a very considerable extent upon the kind of light with which the discs are illuminated The difference between light from a cloudless blue sky and light from the clouds is distinctly shown in the numbers recorded in the paper referred to above.

The numbers obtained may also be different for different observers; the experiment, indeed, forms a test of the colour-perception of the observer.

At the Cavendish Laboratory the colour top is driven by a small water turbine by Baily & Co., of Manchester.

The following table is taken from Lord Rayleigh's paper, being the record of his experiments on July 20, 1870. The circle actually used by him had 192 divisions; his numbers have been reduced to a circle with 100 divisions by multiplying them by 100 and dividing by 192. The second line in each set gives the results of the calculations, while in the first the observed numbers are recorded.

Experiment.

From a series of colour matches with the six given discs, taken five at a time, and compare your results with those given by calculation.

Enter the results as in the above table.

(1)	The water motor referred to in §28 is very convenient for this experiment.