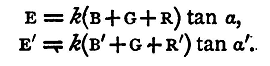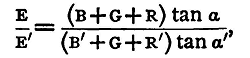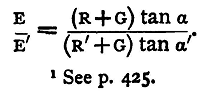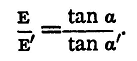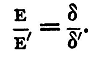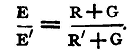Comparison of Electromotive Forces

We may moreover use Ohm's law to compare the electromotive forces of batteries.⁽¹⁾ For suppose we have two batteries; let B, B' be their resistances, E, E' their electromotive forces. Pass a current from the two batteries in turn through two large resistances, R and R' and the galvanometer, and let the deflexions observed be α, α'. Suppose the galvanometer to be a tangent instrument. Then, if k be its reduction factor, G its resistance, we have

Hence

and B+G, B'+G being determined as in the last section, the quantities on the right-hand side are all known.

In practice there are some simplifications. A Thomson's reflecting galvanometer is used, and this is so sensitive that R and R' will need to be enormously large to keep the spot of light on the scale. The values will be probably from eight to ten thousand ohms if only single cells of the batteries in ordinary use be employed. Now the resistance of such a cell will be very small compared with these; an ordinary quart Daniell should be under one ohm; a Leclanché from one to three ohms; and hence we may neglect B and B' as compared with R and R', and we have

This equation is applied in two ways:

(1) The Equal Resistance Method. - The resistance R' is made equal to R, i.e. the two batteries are worked through the same external circuit, and we have then

But if the angles α, α' be not too large, the scale-deflexions of the spot of light are very nearly proportional to tanα and tanα'. Let these deflexions be δ and δ' respectively, then

For this method we do not need to know the galvanometer resistance, but we suppose that the galvanometer is such that the displacement of the spot is proportional to the current

(2) The Equal Deflexion Method. - In this method of working α' is made equal to α, and we have

For this method we require to know G, or, at any rate, to know that it is so small compared with R and R' that we may neglect it. The method has the advantage that we do not assume any relation between the current in the galvanometer and the deflexion produced, except that the same current produces the same deflexion; and this is obviously true whatever be the form of the instrument.

Both methods are open to the objection that the E.M.F. of a battery which is actually producing a current changes from time to time. We shall see in §80 how to compare the E.M.F. of batteries without allowing them to produce a current.

Experiments.

Compare the E.M.F. of the given batteries by the equal resistance and the equal deflexion methods, and taking the E.M.F. of the Daniell's cell as 1.08 volts, find the E.M.F. of the others in volts.

Enter results thus:

Equal Resistance Method. - Resistance used, 10000 ohms. Internal resistance of cells, small.

Equal Deflexion Method. - Deflexion, 83 scale divisions. Galvanometer resistance, small.

1	See p. 425