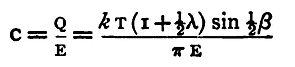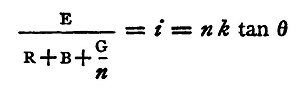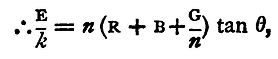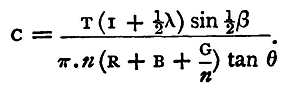Measurement of the Capacity

The methods just described enable us to compare the capacities of two condensers - that is, to determine the capacity of one in terms of that of a standard; just as Poggendorff's method (§80) enables us to determine the E.M.F. of a battery in terms of that of a standard. We have seen, however, in section 74 how to express in absolute measure the E.M.F. between two points; we proceed to describe how to express in absolute measure the capacity of a condenser.

Charge the condenser with a battery of E.M.F., E through a galvanometer, and let β be the throw of the needle, k the reduction factor of the galvanometer, T the time of swing, λ the logarithmic decrement, C the capacity of the condenser, and Q the quantity in the charge.

Then

by formula (4) of p. 469.

Shunt the galvanometer with 1/(n-1)th of its own resistance G, so that 1/nth only of the current passes through the galvanometer; let B be the resistance of the battery; pass a current from the battery through a large resistance R and the galvanometer thus shunted, and let i be the current, θ the deflexion observed. Then we have

for 1/n^th of the current only traverses the galanometer, and produces the deflexion θ;

and

The quantities on the right-hand side of this equation can all be observed, and we have thus enough data to find C.

To express C in absolute measure R, B, and G must be expressed in absolute units.

In practice B will be small compared with R, and may generally be neglected; n will be large, probably 100, so that an approximate knowledge of G will suffice. T may be observed, if it be sufficiently large, by the method of transits (§20), or more simply by noting the time of a large number of oscillations.

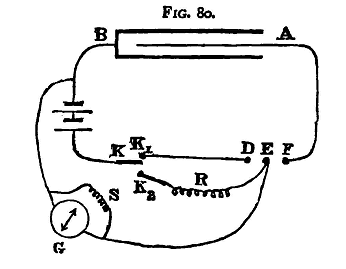
The method assumes that the value of E is the same in the two parts of the experiment A con-stant battery should therefore be used, and the apparatus should be arranged so that a series of alternate observations of β and θ may be rapidly taken. Fig. 86 shows how this may be attained. One plate B of the condenser is connected to one pole of the battery and to the galvanometer; the other plate A is connected to the electrode F of the Morse key. The other pole of the galvanometer is connected to the electrode E, so that in the normal position of the key the two plates are in connection through the galvanometer and the key E.F.

The second pole of the battery is connected to one electrode K of a switch, and the electrode D of the Morse key is connected with another electrode K₁ of the switch. The centre electrode E of the key is connected through the resistance R to the third electrode K₂ of the switch, S is the shunt. With the switch in one position contact is made between K and K₁; on depressing the key the condenser is charged, the galvanometer being out of circuit, and on releasing the key the condenser is discharged through the galvanometer. Note the zero point and the extremity of the throw, and thus obtain a value δ for the throw, in scale divisions.

Shunt the galvanometer, and move the switch connection across to K₂. A steady current runs through the resistance R and the shunted galvanometer; let the deflexion in scale divisions be d; reverse the connections, and repeat the observations several times. The damping apparatus described in the previous section will be found of use. By measuring approximately the distance D between the scale and needle we can find tanθ and sin(0.5β) in terms of d and δ. An approximate value only is required of D from the same reasons as in §71.

Experiment. - Determine absolutely the capacity of the given condenser.

Enter the results thus:

   D = 1230 scale divisions
   δ = 254.5 scale divisions, mean of 4 observations.
   δ = 266 scale divisions, mean of 4 observations.

Whence      β/2 = 2°55.35'
            θ = 6°6.1'

Observations for λ:

    n=15;      C1 = 220;      Cn = 60;
    n=10;      C1 = 210;      Cn = 94;
       Mean value of λ: 0.091.

Observations for T:
20 double vibrations take 64.5 seconds (same value for each of three observations).

    T = 3.225 seconds;
    R = 5000 ohms = 5 x 1012 C.G.S units;
    G = 5600 ohms = 5.6 x 1012 C.G.S. units;

Battery 1 Daniell cell of negligible resistance

    n=100.

Whence        C = 1.012 microfarad.