A Tree Node

This chapter presents a new data structure called a tree, some of its uses and two ways to implement it.

A possible source of confusion is the distinction between an ADT, a data structure, and an implementation of an ADT or data structure. There is no universal answer, because something that is an ADT at one level might in turn be the implementation of another ADT.

To help keep some of this straight, it is sometimes useful to draw a diagram showing the relationship between an ADT and its possible implementations. This figure shows that there are two implementations of a tree:

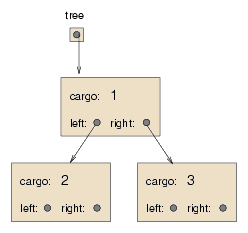
The horizontal line in the figure represents the barrier of abstraction between the ADT and its implementations.

Like lists, trees are made up of nodes. A common kind of tree is a binary tree, in which each node contains a reference to two other nodes (possibly null). The class definition looks like this:

Like list nodes, tree nodes contain cargo: in this case a generic Object. The other instance variables are named left and right, in accordance with a standard way to represent trees graphically:

The top of the tree (the node referred to by tree) is called the root. In keeping with the tree metaphor, the other nodes are called branches and the nodes at the tips with null references are called leaves. It may seem odd that we draw the picture with the root at the top and the leaves at the bottom, but that is not the strangest thing.

To make things worse, computer scientists mix in yet another metaphor: the family tree. The top node is sometimes called a parent and the nodes it refers to are its children. Nodes with the same parent are called siblings, and so on.

Finally, there is also a geometric vocabulary for taking about trees. I already mentioned left and right, but there is also "up" (toward the parent/root) and down (toward the children/leaves). Also, all the nodes that are the same distance from the root comprise a level of the tree.

I don't know why we need three metaphors for talking about trees, but there it is.