| 2-1 |
Given a charge of q coulombs in free space at the origin in a system of x, y, and z coordinates, determine in terms of q
(a) The electric flux density.
(b) The electric field intensity.
(c) The voltage gradient at x=3, y=4, and z=12 m.
HINT: 
|
| 2-2 |
In Problem 2-1, what is the voltage between two points at the following locations
(a)
(i) x=3, y=4, z=12 m, and (ii) x=0, y=5, z=12 m.
(b)
(i) x=1.5, y=2.0, z=6.0 m, and (ii) x=4.0, y=12.0, z=3.0m.
|
| 2-3 |
Assume the earth to be a sphere having a radius of 6,380 km, Determine
(a) The capacitance of the earth.
(b) The potential of the earth if it were completely isolated in space and carried a uniformly distributed charge of 1 coulomb.
(c) The energy stored in space due to the charge of 1 coulomb on the earth's surface.
(d) The potential gradient at the earth's surface due to the 1-coulomb charge.
|
| 2-4 |
Given two concentric conducting spherical shells of negligible thickness having diameters of 15 cm and 10 cm. The medium between these shells and that external to them is free space. A surface integral of electric field intensity obtained between the shells gives a value of 1.13 x 106m v, whereas a surface integral taken over the outer surface of the outer spherical shell also yields a value of 1.13 x 106 m v. In addition, the surface integral of electric field intensity taken over the inner surface of the inner shell has a value of zero. Determine
(a) The charge within the inner shell.
(b) The charge within the outer shell.
(c) The charge on the inner shell.
(d) The charge on the outer shell.
|
| 2-5 |
Under a different set of conditions the following values of surface integrals of electric field intensity in meter volts are obtained for the concentric spherical shells of Problem 2-4.
(a) Over the outer surface of the outer shell, zero.
(b) Over the outer surface of the inner shell, 1.13 x 105.
(c) Over the inner surface of the inner shell, zero.
Determine
(i) The charge within the inner shell.
(ii) The charge within the outer shell,
(iii) The charge on the inner shell.
(iv) The charge on the outer shell.
|
| 2-6 |
Under a third set of conditions the following values of surface integrals of electric field intensity in meter volts are obtained for the concentric spherical shells of Problem 2-4.
(a) Over the outer surface of the outer shell, 1.13 x 105.
(b) Over the inner surface of the outer shell, 1.13 x 105.
(c) Over the inner surface of the inner shell, 1.13 x 105.
Determine
(i) The charge within the inner shell,
(ii) The charge within the outer shell,
(iii) The charge on the inner shell,
(iv) The charge on the outer shell.
|
| 2-7 |
If the space between the concentric spherical shells is filled with transformer oil, the relative dielectric constant of which is 2.24, determine the values of the surface integrals if the charges are at the same locations as in Problem 2-6. The medium surrounding the outer sphere is free space and that enclosed by the inner sphere is free space.
|
| 2-8 |
Given a conducting sphere isolated in free space carrying a uniformly distributed charge q. The radius of the sphere is a meters. Determine the energy density of the electric field at
(a) The surface of the sphere,
(b) A point external to the surface and a distance r from the center of the sphere.
|
| 2-9 |
Determine the energy stored in the space between the equipotential surfaces at r1 and r2 m from the center of the sphere and external to the surface of the sphere of Problem 2-8.
|
| 2-10 |
Repeat Problem 2-9 for the condition that the space between r1 and r2 is occupied by a medium that has a relative dielectric constant kr.
|
| 2-11 |
Determine the maximum energy density that can be supported by air on the basis that breakdown occurs at E = 3 million v per m. What is the charge density at that value of electric field intensity ?
|
| 2-12 |
Determine the capacitance of two concentric spheres if the diameter of the inner sphere is 10 cm and that of the outer sphere is 11 cm if the dielectric is
(a) Air.
(b) Transformer oil.
|
| 2-13 |
Determine the charge on the spheres in Problem 2-12 when the voltage between them is 5,000 v and the dielectric is
(a) Air.
(b) Transformer oil.
|
| 2-14 |
What is the electric field intensity at the surface of the inner sphere and at the surface of the outer sphere in Problem 2-12, when the applied voltage is 5,000 v and the dielectric is
(a) Air.
(b) Transformer oil.
|
| 2-15 |
Given two concentric spheres the outer sphere of which has a fixed radius r2. Determine r1 the radius of the inner sphere in terms of r2 such that the maximum electric field intensity in the dielectric is a minimum for a given applied voltage between the spheres.
|
| 2-16 |
Repeat Problem 2-15 for concentric cylinders.
|
| 2-17 |
The conductor of a 230-kv single-conductor oil-impregnated cable has a diameter of 1.835 in. and the insulation surrounding the conductor is 0.925 in. thick. A lead sheath 0.170 in. in thickness tightly surrounds the insulation.
The relative dielectric constant kr of the insulation is 3.5. This cable is one of three operating at a 3-phase, 60-cycle voltage of 230 kv between the conductors of the cable. The voltage between the conductor and the sheath of each cable is therefore 132.5 kv. Determine for a length of one mile of cable
(a) The capacitance.
(b) The energy stored in the cable at a maximum emf of 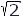 x 132.5 kv. x 132.5 kv.
(c) The capacitive reactance in ohms at 60 cycles.
(d) The charging current at 132.5 kv and 60 cycles.
(e) The electric field intensity in
(i) Volts per meter,
(ii) Volts per inch at
(a') The surface of the conductor.
(b') The inner surface of the lead sheath when the applied voltage is 2 x 132.5kv.
|
| 2-18 |
A 2,400-volt capacitor is rated at 15 kva at 60 cps. The thickness of the dielectric is 0.008 in. and the relative dielectric constant is 5.20. Determine
(a) The area of the plates in this capacitor.
(b) The dielectric loss if the dissipation factor is 0.25 percent.
(c) The Q of the capacitor.
|
| 2-19 |
The relative dielectric constant of the dielectric in a ceramic capacitor is 1,000. Determine the ratio of area to thickness of the dielectric if the capacitor has a capacitance of 1,000 μf (a) with the meter as the unit of length (b) with the inch as the unit of length.
|
| 2-20 |
Measurements made with a capacitance bridge on a liquid dielectric test cell at a frequency of 1,000 cps gave the following results
(a) Cell empty
C = 110.0 mmf DF = 0.0000
(b) Cell filled with liquid dielectric
C = 246.5 mmf DF = 0.0030
(i) Determine the equivalent parallel capacitance C and the equivalent
parallel resistance R on the basis of the equivalent circuit of Fig.
2-25(e)
(a') when the cell is empty
(b') when the cell is filled with the dielectric liquid, (ii) Determine the quality factor Q for
(a') The empty cell.
(b') The filled cell, (iii) Determine the complex dielectric constant of the liquid dielectric.
|
| 2-21 |
Two parallel plane plates having an area of 20 sq ft each and a separation of 3 in. are charged to a potential difference of 100,000 v. The source of potential
is removed and the separation of the plates is increased from 3 to 5 in. Determine
(a) The potential difference between plates when separated 5 in.
(b) The energy required to increase the separation from 3 to 5 in. (neglect fringing).
|
| 2-22 |
A constant potential difference of 100,000 v is maintained between the plates in Problem 2-21 while the spacing decreases from a value of 3.0 to one of 1.5 in. Neglect fringing and determine
(a) The mechanical energy.
(b) The change in the stored energy.
(c) The average electrical power input if this change in spacing takes place in 0.01 sec.
(d) The amount of the electric power in part (b) that is absorbed by the dielectric and the amount of electric power that is converted into mechanical power. (Is this motor power or generator power ?)
|
| 2-23 |
A variable air capacitor has its rotor free to rotate completely. The minimum and maximum values of capacitance are 16 x 10-12 and 250 x 10-12 farads. Assume the capacitance to vary linearly with angular displacement and that in one-half revolution the capacitance goes from minimum to maximum and returns from maximum to minimum during the next half revolution. A constant d-c potential of 700 v is applied to this capacitor. Assume the angular displacement to be zero when the capacitance is a minimum.
(a) Plot a graph of
(i) Capacitance vs angular displacement, (ii) Torque vs angular displacement. (iii) Current vs angular displacement when the rotor is driven at a speed of 3,600 rpm.
(b) Determine the approximate power consumed in a resistor of one megohm connected in series with this capacitor when the rotor is driven at 3,600 rpm.
(c) How much of the power in part (b) is furnished (i) By the d-c source? (ii) By the device that drives the rotor of the capacitor?
|
| 2-24 |
The dielectric in the cable of Problem 2-17 has a resistance of 1015 ohms per cm cube at a certain temperature. Determine the resistance of the insulation in one mile length of this cable.
|


 Capacitance and Related Effects
Capacitance and Related Effects  Problems
Problems





 Capacitance and Related Effects
Capacitance and Related Effects  Problems
Problems


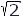 x 132.5 kv.
x 132.5 kv.