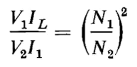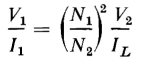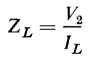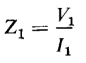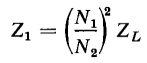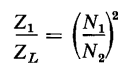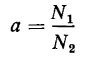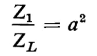Impedance Ratio

In many problems that involve transformers it is convenient to refer the impedance in one side of the transformer to the other side of the transformer.

Figure 6-5. Equivalent circuits of (a) ideal transformer and connected load impedance; (b) load impedance referred to primary side of transformer.

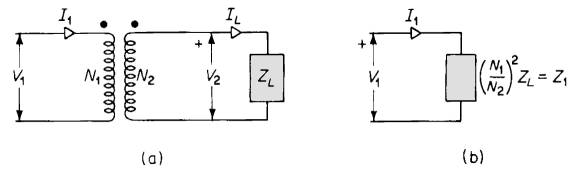
For example, Fig. 6-5(a) shows an ideal transformer with a load impedance of Z_L ohms connected across its secondary terminals. The load impedance referred to the primary is the value of impedance that, if connected directly across the source of voltage V₁, would draw the same value of current I₁ as the transformer with its connected load impedance Z_L. This is shown in Fig. 6-5(b).

When Eq. 6-14 is divided by Eq. 6-17 the result is

or

[6-18]

But the load impedance is

[6-19]

and an impedance that would draw a current of I₁ amp when connected directly across the source of voltage of V₁ v must have a value of

[6-20]

A comparison of Eqs. 6-18, 6-19, and 6-20 shows that

[6-21]

where Z₁ is the value of the load impedance referred to the primary of the transformer. The impedance ratio is, therefore

[6-22]

or the square of the turns ratio of the transformer.

The turns ratio of a transformer is sometimes represented by the letter a, which means that

[6-23]

and the impedance ratio is

[6-24]