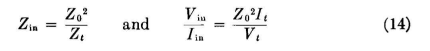Important Transmission-line Equations

Author: Edmund A. Laport

The following equations, derived from transmission-line theory and proved in the classical literature on this topic, have frequent utility in the design of systems, and are grouped here for reference.

In general

At radio frequencies, when ω becomes very large with respect to other factors

When the field of the transmission line is entirely within an isotropic dielectric medium having an inductivity, or dielectric constant, €,

The propagation constant y is in general complex;

At radio frequencies and with lossless lines, 7 becomes essentially a phase angle per unit length.

The velocity of propagation of transverse electromagnetic waves in systems of parallel linear conductors with air dielectric is equal to c, which is the velocity of light in free space (3·10⁸ meters per second).

For a line in an isotropic dielectric ε, the velocity of propagation is

When a radio-frequency line of length βl degrees (or radians) is terminated in a complex impedance Z_t the input impedance Z_in is, in general, complex, in accordance with the equation

When Z_t <> Z₀, there is reflection from the termination. The reflection factor is, in general, complex, and is specified as follows:

When Z_t = 0 (short circuit),

When Z_t = (open circuit),

For a line of length βl = π radians = 180 degrees (one-half wavelength)

also

For a line of length βl = π/2 = 90 degrees (one-quarter wavelength)

This is an impedance-inverting circuit with a 90-degree change in relative phase between input and output currents and potentials. When βl = 45 degrees (one-eighth wavelength) and Z_t = R_t + _j0,

and in general |Z_in| = |Z₀| for all values of R_t, positive and negative, from 0 to . (Only the angle of Z_in varies with R_t.)

The standing-wave ratio Q on a transmission line increases with increasing inequality between Z_t and Z₀ both in phase and in magnitude.

This equation for Q is useful when transmission lines are used as high-Q resonant circuits.

When a section of transmission line is used as a transformer to match an impedance Z_t = R_t ± jX_t with another impedance Z_in = R_in ± jX_in, the characteristic impedance Z₀₀ of the transforming section is

and its electrical length must be

in which

In all the preceding equations the following symbols apply:

1)	1 neper = 1 hyperbolic radian = 8.686 decibels, corresponding to a current (or voltage) ratio of 2.7182+ = e.