Single-phase to Polyphase Transformations

Author: Edmund A. Laport

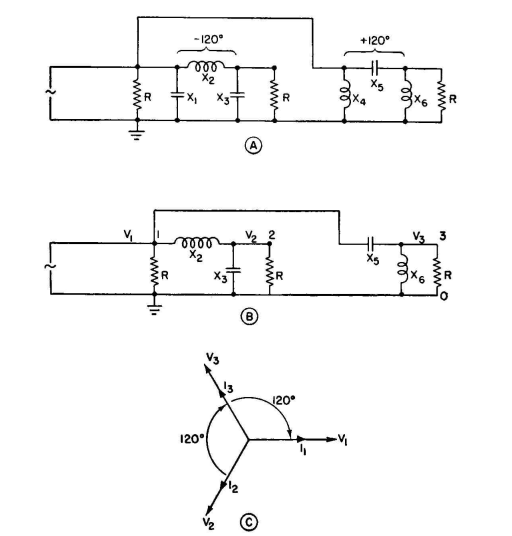
To derive a system of balanced three-phase potentials from a constant-frequency single-phase generator, all that is required is to consider the original source as one of the phases. The second phase is derived from the original source by connecting it to a 1-to-l phase-shifting network with a phase shift of -120 degrees and terminated by a resistance R. The third phase is derived in the same manner by bridging the source with a second phase-shifting network with a phase shift of +120 degrees, with a 1-to-l ratio, and terminated in the same value of resistance R.

Fig. 5.45

If the original source has also a resistance R directly across it as the load for the first phase (see Fig. 5.45A), the potentials across all three resistors will be equal in magnitude and at successive 120-degree angles. As shown, one side of each resistor is common, so that the balanced three-phase Y arrangement is obtained, as represented in Fig. 5.45C.

The circuit of Fig. 5.45B is the same as that of Fig. 5.45A after taking into account the fact that X₄ = X₁. Since both reactances are directly in parallel, they mutually become infinite in impedance owing to antiresonance and are eliminated from the real circuit. The other elements are unchanged in value.

If a delta three-phase connection be desired, the resistors R can all be removed and three other resistors with a value R₁ can be substituted but connected, respectively, between points 1 and 2, 2 and 3, and 3 and 1. To maintain correct loadings equivalent to R of the Y arrangement, for which the design was derived, R₁ = 3R.

It is evident from the preceding examples that, with networks of this type having fixed values for the reactances, the phase shift will vary with any deviations from the value R which terminates each phase. Therefore, true balanced three-phase potentials are dependent upon the load resistances for each phase remaining constant at the value for which the networks were designed.

It is apparent that other polyphase relations may be derived by the same principle. In fact, any number of vectors at any angle and with any magnitude can be developed from the single-phase source by employing paralleled or cascaded networks of the proper phase shift and transformation ratio, each terminated in some preselected value of resistance, according to the desired power division among the loads.

The design of a feeder system for a multielement directive antenna of the type so frequently required for medium-frequency broadcasting stations is in fact the design of a single-phase to polyphase network, the number of phases being determined by the number of radiators that are to be fed. The relative phases of the currents in the several radiators have to be derived from a common single-phase generator, which is usually the main feeder, or sometimes the transmitter itself.

In general, the impedances of the inputs to the several radiators, when the system is performing correctly so as to obtain the specified radiation pattern, are unequal. Therefore, the power transmitted through each phase to its associated radiator is different from that in the others. The feeder system as a whole is for that reason an unbalanced polyphase circuit, unbalance meaning that the phase relations may be unsym-metrical and the powers in the several phases unequal.

It is evident that the excitation for any one phase can be derived from any other phase instead of connecting every phase directly across the main source. The impedance-matching and the power-dividing networks can be distributed along a series of transmission lines running from radiator to radiator instead of bringing separate transmission lines from each radiator to the transmitter. Both methods are used, the choice being one of cost and convenience. The individual-feeder method may often be preferred when switching is required to change the pattern for a multielement array, as is often done for day and night operation.