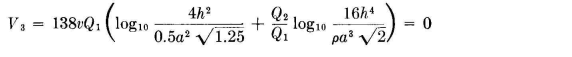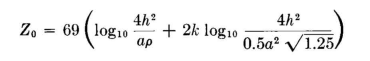One or More of the Conductors Are Grounded

Author: Edmund A. Laport

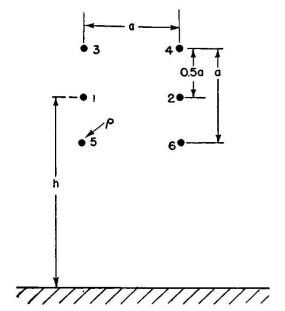
Unbalanced lines employing both high-potential and grounded wires, all parallel to ground, can be computed by equating the potentials on the grounded wires to zero. In such cases another step of procedure is necessary to solve for the charge ratios among the various wires and the ground charge, since in practical systems of this type there is always some stray capacitance direct from the high-potential wires to ground, as well as to the grounded wire(s).

To illustrate the procedure, consider a six-wire unbalanced line having the sectional geometry of Fig. 6.5. The two middle wires on each side are in parallel at high potential. The four outer wires located at the corners of a square are grounded. The configuration is located at an average height h which is sufficiently large with respect to a to allow the convenience of employing a constant value of h for all the wires with negligible numerical error.

We see that there is symmetry to this problem, which makes evident at once that the charges on the wires on the left will be the same as for those on the right. If h is sufficiently large with respect to a, as assumed and as justified in the majority of practical applications, there will be symmetry of charge distribution across the upper and lower halves of the configuration. In other words, the total ground-wire charge will be equally divided among the four grounded wires.

Fig. 6.5

From these considerations the potential equations are written as follows: For

For the four grounded wires 3, 4, 5, and 6,

or

Solving for the ratio

Making this substitution in the first equation permits the desired information to be derived. Since Q₁ is the charge on one high-potential wire and Q₂ the charge on one grounded wire, the characteristic impedance becomes (using the manipulations previously employed and remembering that there are two high-potential wires in parallel),

It is always of importance to know the ratio of the return current in the grounded wires to the current in the high-potential wires. In this example, where there are four grounded wires each with charge Q₂ and two high-potential wires each with charge Q₁, the total charge ratio on the wires (and therefore the current ratio) will be 4Q₂/2Q₁ = 2k. Therefore, if I is the total current in the high-potential wires, the total return current in the grounded wires will be 2kI.

That portion of the total current I which does not return in the grounded wires must return through the ground. Therefore the ground-return current I_g = I(1-2k).