You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents Multivariate Data Modeling Factor Analysis Factor Analysis
Index
See also: PCA 

Factor Analysis

Factor analysis has a long history with its root in psychology. The first development was reported by Hotelling in 1933. Later on, other authors extended this method, finally resulting in a range of various methods which are difficult to overlook. An excellent book on factor analysis was published by Paul Horst [Horst 1965].

One of the possible definitions has been given by Malinowski:
 


The principle behind factor analysis is quite simple, although the concrete realization depends on the requirements of the specific situation, and may be quite demanding: in principle, a data matrix X is split up into a product of two data matrices:

X = U V

The matrices U and V are called scores and loading matrices, respectively. This can be visualized by the following figure:

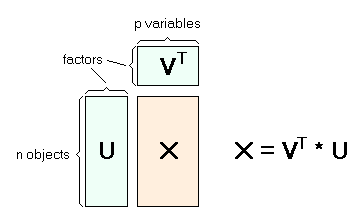
Using this approach involves factors which may be useless for tangible problems, since one of the major goals of factor analysis is to provide factors which are related in some way to "real" factors. So the matrices U and V are rather abstract matrices which provide little to no improvement concerning the interpretation of the original matrix. It is therefore necessary to come up with a way to find factors which are closely related to reality. Since the theoretical split into the matrices U and V has many solutions, we need some additional criteria to guide the decomposition of the original data matrix X.

The following general rules for finding suitable factors are usually applied:
 


Last Update: 2006-Jän-17