 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Math Background Math Background  Introduction to Probability Introduction to Probability  Counting Rules Counting Rules |
|
| See also: events and probability |   |
When selecting elements of a set, the number of possible outcomes depends on the conditions under which the selection has taken place. There are at least 4 rules to count the number of possible outcomes:
n1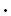 n2*
...
n2*
...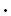 nj.
nj.
Given a single set of n distinctively different elements, you wish to select k elements from the n and arrange them within k positions. The number of different permutations of the n elements taken k at a time is denoted Pkn and is equal to
![]() .
.
![]() ,
,
The numerator gives the permutations of the n elements. The terms in
the denominator remove the duplicates due to the same assignments in the
k sets (multinomial coefficients).
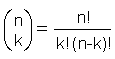 .
.The combination rule is a special application of the partition rule, with j=2 and n1=k. From n=n1+n2 it follows that n2 can be replaced by (n-n1). Usually the two groups refer to the two different groups of selected and non-selected samples. The order in which the n1 elements are drawn is not important, therefore there are fewer combinations than permutations (binomial theorem).
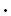 2
2 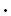 3
3
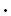 ...(n-2)
...(n-2) 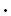 (n-1)
(n-1)
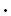 n. (0! is defined as 1).
n. (0! is defined as 1).
Last Update: 2006-Jšn-17