 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
| See also: signal-to-noise ratio, mathematical details |   |
Time-averaging is a simple and efficient method of increasing the signal-to-noise ratio (S/N ratio) of a signal. This method is applicable to all situations where the signal is stable over several hundred measuring cycles. The signal is registered repeatedly and summed up. Since noise contributes in a probabilistic manner, whereas the net signal always contributes to a signal in the same direction, noise will finally cancel out.
It can be shown that the noise decreases with the square root of the number of repeated measurements; thus the S/N ratio increases accordingly:
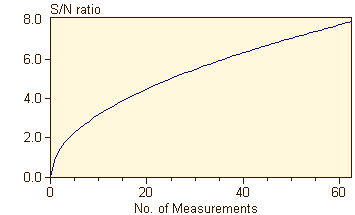
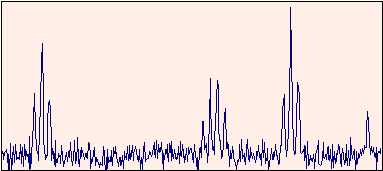
Below you see a signal obtained from a single measurement. Three peak groups are barely recognizable in the noisy background.

If this measurement is repeated 36 times, the signal to noise ratio increases by a factor of 6, and the underlying signal can be peceived clearly:
You can experiment with time averaging by clicking on this![]() in order to see an example dealing with NMR (nuclear magnetic resonance)
spectroscopy. NMR spectroscopy is used to elucidate chemical structures.
It is comparatively insensitive and needs "large" amounts of samples (in
the mg range, which by a factor 1000 to 1000000 is higher than that needed
by other methods). If the amount of substance is small, one can try to
enhance the sensitivity by time-averaging the signal.
in order to see an example dealing with NMR (nuclear magnetic resonance)
spectroscopy. NMR spectroscopy is used to elucidate chemical structures.
It is comparatively insensitive and needs "large" amounts of samples (in
the mg range, which by a factor 1000 to 1000000 is higher than that needed
by other methods). If the amount of substance is small, one can try to
enhance the sensitivity by time-averaging the signal.
Last Update: 2004-Jul-03