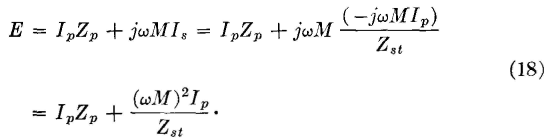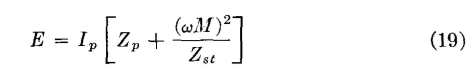| Electrical Communication is a free textbook on the basics of communication technology. See the editorial for more information.... |

|

Home  Electrical Fundamentals of Communication Electrical Fundamentals of Communication  Inductively Coupled Circuits Inductively Coupled Circuits |
|||






|
|||
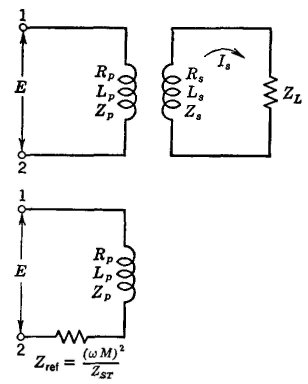
Inductively Coupled CircuitsThe current in the primary of a coil will induce a voltage in the secondary of the coil. If the secondary is open and no appreciable current flows through the secondary distributed capacitance, the effect of the secondary may be neglected. If the secondary is closed through some load impedance ZL so that current does flow, then the effect of this current is felt in the primary, and the primary current is altered. Since the effect of a load connected to the secondary is to alter the current in the primary, the effect of the load is like connecting some impedance into the primary. This value of impedance is called a reflected impedance and is indicated in Fig. 11.
The magnitude and angle of the reflected impedance can be found as follows: Referring to equation 8 the voltage induced in the secondary will lag 90° behind the current in the primary, or Es = -jωMIp, and this must equal IsZst,, where Zst is the total secondary impedance, including the impedance of the secondary of the coil and the load. Equating these two expressions, and solving for Is gives
The voltage E must equal the sum of the voltage drop across the coil and voltage induced in the primary by the secondary, because this induced voltage must oppose flow of primary current. Thus,
This equation can be written
which states that the effect of the closed secondary is to couple a load of impedance (ωM)2/Zst into the primary. All solutions must consider both the magnitudes and angles. To find the current flow in the secondary of Fig. 11 the steps are as follows: 1. Find the reflected impedance (ωM)2/Zst, where ω = 2πf, M is the mutual inductance in henrys, and Zst is the total secondary impedance. 2. Find the total impedance between points 1-2, by adding the reflected impedance to the impedance of the primary of the coil. 3. Find the primary current by dividing the impressed voltage E (which may well be taken as the reference vector) by the total impedance between points 1-2. 4. Find the voltage induced in the secondary by the expression Es = -jωMIp. 5. Find the secondary current by dividing this induced voltage by the total secondary impedance.
|
|||
Home  Electrical Fundamentals of Communication Electrical Fundamentals of Communication  Inductively Coupled Circuits Inductively Coupled Circuits |
|||
Last Update: 2011-05-30