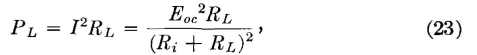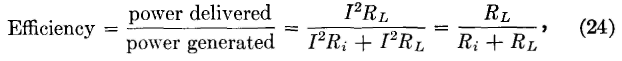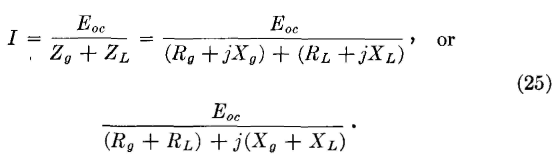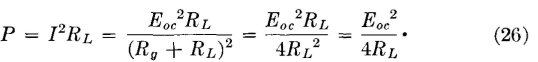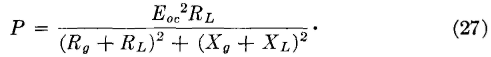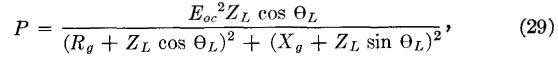Maximum Power Transfer

The principle of maximum power transfer can be illustrated by a simple example. Suppose that a battery of constant open-circuit voltage E_oc and internal resistance R_i is connected directly to a load resistor R_L. It is desired to find the value of R_L such that the maximum power is transferred from the battery to the load.

The current flowing will be

and the power P_L delivered to the load resistor R_L will be

where P_L will be in watts, when the other units are amperes, volts, and ohms.

If equations 22 and 23 are examined, the power P_L delivered to the load will be seen to approach zero if R_L approaches either zero or infinity in value. There is, accordingly, some intermediate point where the power transferred is maximum. This can be found by differentiating equation 23 and equating to zero, or by plotting a curve of equation 23. By either method it is found that maximum power is transferred from the battery to the load when the load resistance equals the internal resistance of the battery.

Figure 12. Percent of short-circuited power Eoc2/Ri and efficiency for different values of RL/Ri.

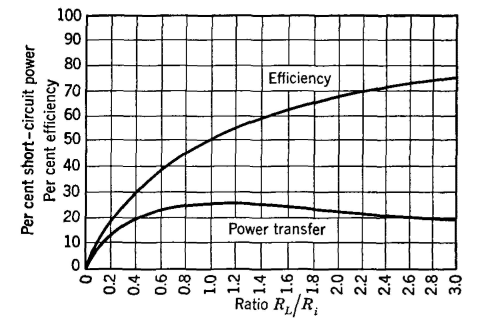
The relations just discussed are plotted in Fig. 12. The maximum power that can be developed by the battery is that produced when it is short circuited. The per cent of this delivered to the load is plotted against the ratio of the load resistance R_L to the battery internal resistance R_i, and maximum power transfer occurs when R_L = R_i. The efficiency of power transfer is

and, when R_L =R_i, the efficiency is 50 per cent; that is, half of the power generated is lost in the battery, and half is delivered to the load.

In alternating-current circuits the power transferred from a generator of open-circuit voltage E_oc and internal impedance Z_g to a load of impedance Z_L will be P = I²R_L, where

If the reactance X_L of the load is equal in magnitude and opposite in sign to the internal reactance X_g of the generator, then the reactances cancel, and the relations previously considered apply; that is, maximum power transfer occurs when R_L = R_g, and the efficiency is 50 percent. Impedances, which have equal resistance components and reactance components equal in magnitude but opposite in sign, are defined¹ as conjugate impedances. For conjugate impedances the maximum power transferred becomes

If the generator internal impedance and the load impedance are not conjugates, the power transferred is P = I²R_L, where I is as given by equation 25. Thus, the power transferred is

When Z_g and Z_L are equal both in magnitude and angle (that is, R_g = R_L, and X_g = X_L), then equation 27 may be written

In communication circuits the following problem is often encountered: a load of impedance Z_L is to be connected to a generator of internal impedance Z_g. It is not possible to obtain a condition of conjugate impedances. Instead, the generator and load must be connected through a transformer that can be used to alter the magnitude only of the impedance. If the magnitude, but not the angle of an impedance can be altered, the relations for maximum power can be determined by rewriting equation 27 as follows

and by differentiating this expression and equating to zero.¹⁴ The solution shows that when the magnitude Z_L but not the angle θ_L of a load impedance can be varied, maximum power will be transferred from a generator of internal impedance Z_g when the magnitude of Z_L equals the magnitude of Z_g.