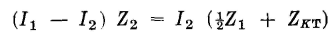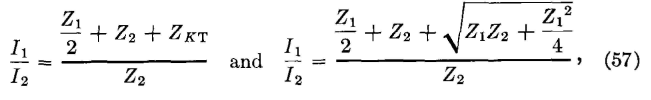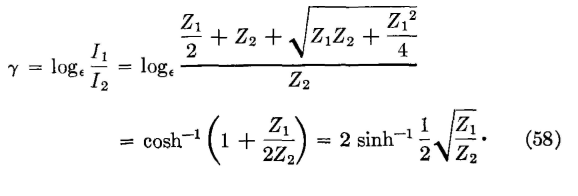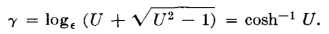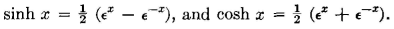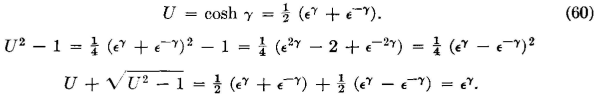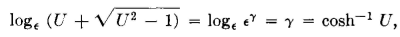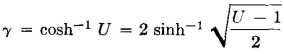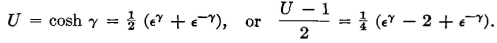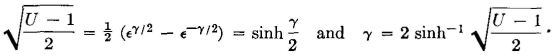Electrical Communication is a free textbook on the basics of communication technology. See the editorial for more information....

Home Electric Networks Propagation Constant of a Transducer
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

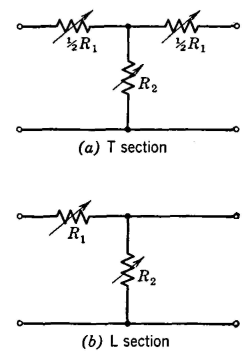
Propagation Constant of a Transducer

As an electromagnetic wave, such as an audio-frequency signal wave, travels along a network such as Fig. 6, two important phenomena occur. First, the magnitudes of the voltage and current at the input terminals will not be the same as the magnitudes of the voltage and current at the output terminals. For a network such as Fig. 6 the output voltages and currents will be less than the input voltages and currents, and attenuation, defined1 as "a decrease in amplitude," will have occurred. Second, because time is required for a signal wave to travel through a network, the output voltage will not be in phase with the input voltage, and the output current will not be in phase with the input current. Thus, a time delay and a phase shift will occur.

Figure 23. Unbalanced attenuators commonly used.

The magnitudes of the attenuation and phase shift that occur are determined by the propagation constant of a transducer, defined1 as "the natural logarithm of the ratio of the current entering the transducer to the current leaving the transducer, when the transducer is terminated in its iterative impedances." This definition applies to symmetrical networks; corresponding definitions for unsymmetrieal networks will be found in reference 1. The propagation constant is usually represented by γ and is a complex number. By definition,1 the real part of the propagation constant is the attenuation constant (usually represented by α), and the imaginary part is the phase constant (usually represented by β).

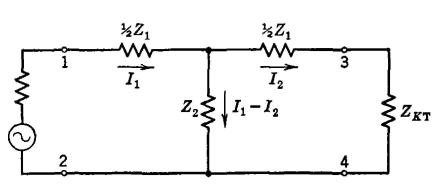
Figure 24. Circuit for determining the propagation constant of a transducer.

If the current entering the network of Fig. 24 is I1 and if the current leaving the network is I2, the current through the shunt element will be I1-I2- It can be written that

and that

when the value of ZKT from equation 45 is substituted. From the definition for propagation constant,

The mathematical proof of these relations is given in detail in reference 5, on page 123, and in appendix C, from which the following has been taken: Assume that U = 1 + (Z1/2Z2). Then, equation 58 may be written

From fundamental mathematical relations,

Then, from equation 59,

Hence,

and when the value U = 1 + (Z1/2Z2) is substituted, the first hyperbolic term of equation 58 is proved.

The proof that

is as follows:

From equation 60,

Then,

When the value of U is substituted, the last part of equation 58 is proved.


Home Electric Networks Propagation Constant of a Transducer

Last Update: 2011-05-30